Câu hỏi:
11/03/2024 75
Cho \[A = \frac{1}{{101}} + \frac{1}{{102}} + \frac{1}{{103}} + ... + \frac{1}{{199}} + \frac{1}{{200}}\]. Chứng minh \(\frac{1}{2} < A < 1.\)
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải:
Ta có:
\(\frac{1}{{200}} < \frac{1}{{101}} < \frac{1}{{100}}\)
\(\frac{1}{{200}} < \frac{1}{{102}} < \frac{1}{{100}}\)
\(\frac{1}{{200}} < \frac{1}{{103}} < \frac{1}{{100}}\)
…
\(\frac{1}{{200}} < \frac{1}{{199}} < \frac{1}{{100}}\)
Suy ra:
\(\frac{1}{{200}} + \frac{1}{{200}} + \frac{1}{{200}} + ... + \frac{1}{{200}} < \frac{1}{{101}} + \frac{1}{{102}} + \frac{1}{{103}} + ... + \frac{1}{{199}} < \frac{1}{{100}} + \frac{1}{{100}} + \frac{1}{{100}} + ... + \frac{1}{{100}}\)
Hay \[99.\frac{1}{{200}} < \frac{1}{{101}} + \frac{1}{{102}} + \frac{1}{{103}} + ... + \frac{1}{{199}} < 99.\frac{1}{{100}}\]
\(\frac{{99}}{{200}} + \frac{1}{{200}} < \frac{1}{{101}} + \frac{1}{{102}} + \frac{1}{{103}} + ... + \frac{1}{{199}} + \frac{1}{{200}} < \frac{{99}}{{100}} + \frac{1}{{100}}\)
\(\frac{{100}}{{200}} < \frac{1}{{101}} + \frac{1}{{102}} + \frac{1}{{103}} + ... + \frac{1}{{199}} + \frac{1}{{200}} < \frac{{100}}{{100}}\)
Do đó \(\frac{{100}}{{200}} < A < \frac{{100}}{{100}}\)
Suy ra \(\frac{1}{2} < A < 1.\)
Hướng dẫn giải:
Ta có:
\(\frac{1}{{200}} < \frac{1}{{101}} < \frac{1}{{100}}\)
\(\frac{1}{{200}} < \frac{1}{{102}} < \frac{1}{{100}}\)
\(\frac{1}{{200}} < \frac{1}{{103}} < \frac{1}{{100}}\)
…
\(\frac{1}{{200}} < \frac{1}{{199}} < \frac{1}{{100}}\)
Suy ra:
\(\frac{1}{{200}} + \frac{1}{{200}} + \frac{1}{{200}} + ... + \frac{1}{{200}} < \frac{1}{{101}} + \frac{1}{{102}} + \frac{1}{{103}} + ... + \frac{1}{{199}} < \frac{1}{{100}} + \frac{1}{{100}} + \frac{1}{{100}} + ... + \frac{1}{{100}}\)
Hay \[99.\frac{1}{{200}} < \frac{1}{{101}} + \frac{1}{{102}} + \frac{1}{{103}} + ... + \frac{1}{{199}} < 99.\frac{1}{{100}}\]
\(\frac{{99}}{{200}} + \frac{1}{{200}} < \frac{1}{{101}} + \frac{1}{{102}} + \frac{1}{{103}} + ... + \frac{1}{{199}} + \frac{1}{{200}} < \frac{{99}}{{100}} + \frac{1}{{100}}\)
\(\frac{{100}}{{200}} < \frac{1}{{101}} + \frac{1}{{102}} + \frac{1}{{103}} + ... + \frac{1}{{199}} + \frac{1}{{200}} < \frac{{100}}{{100}}\)
Do đó \(\frac{{100}}{{200}} < A < \frac{{100}}{{100}}\)
Suy ra \(\frac{1}{2} < A < 1.\)
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Bạn An đọc một cuốn sách trong ba ngày. Ngày thứ nhất An đọc được \(\frac{1}{3}\) số trang sách, ngày thứ hai An đọc được \(\frac{5}{8}\) số trang sách còn lại, ngày thứ ba đọc nốt 90 trang còn lại. Hỏi cuốn sách có bao nhiêu trang?
Câu 2:
Cho hình vẽ sau:
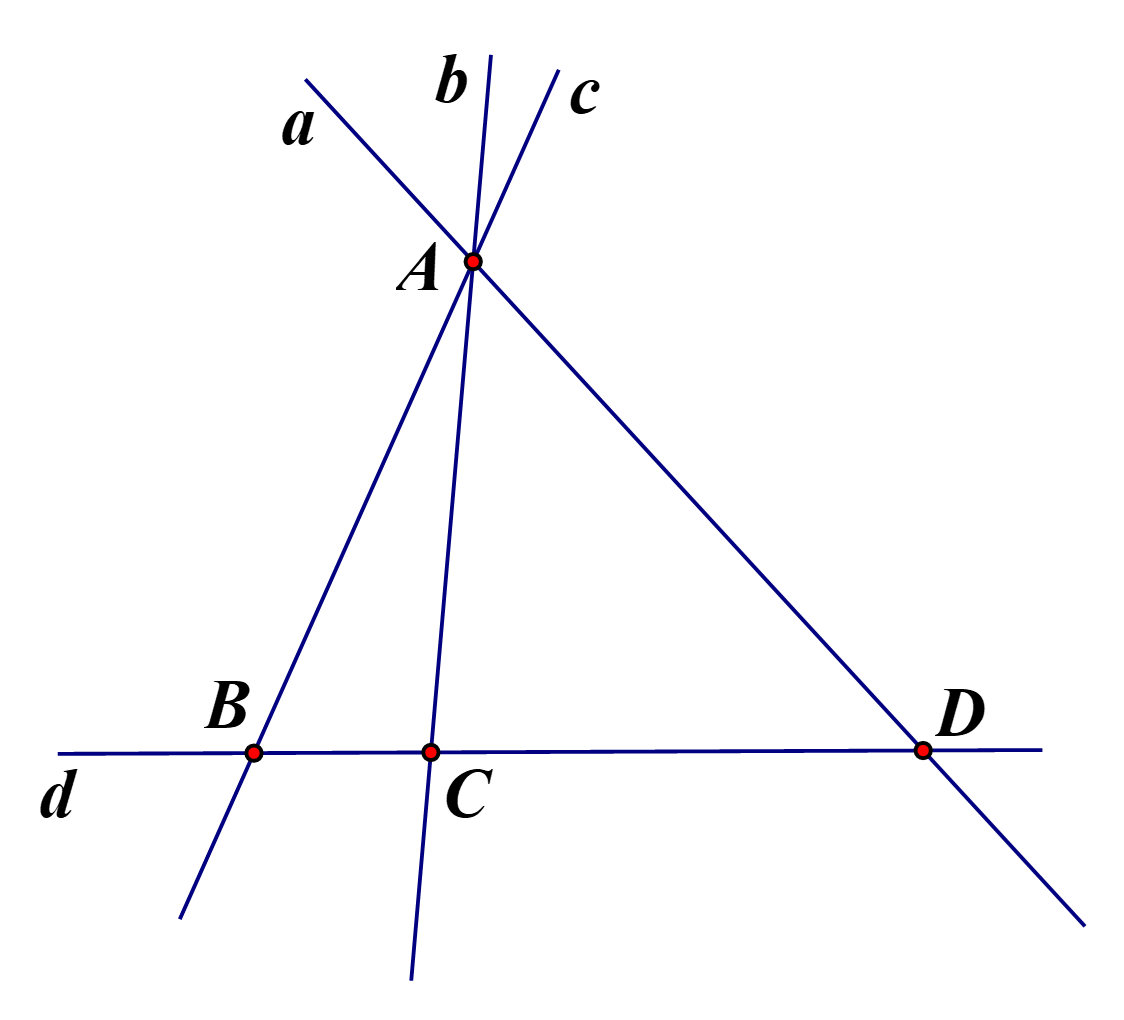
a) Có bao nhiêu đường thẳng đi qua điểm A? Kể tên.
b) Điểm C nằm trong góc nào?
c) Trên hình vẽ biết điểm C nằm giữa hai điểm B và D. Cho BC = 1 cm, CD = 3 cm. Hỏi điểm C có phải là trung điểm của BD không? Tính BD.
Cho hình vẽ sau:

a) Có bao nhiêu đường thẳng đi qua điểm A? Kể tên.
b) Điểm C nằm trong góc nào?
c) Trên hình vẽ biết điểm C nằm giữa hai điểm B và D. Cho BC = 1 cm, CD = 3 cm. Hỏi điểm C có phải là trung điểm của BD không? Tính BD.
Câu 3:
Tìm x biết
a) x : 2,2 = (28,7 – 13,5).2;
b) \(\frac{1}{2}x + \frac{2}{3}(x - 1) = \frac{1}{3}\);
c) \(\frac{2}{3}x:\frac{1}{5} = 1\frac{1}{3}:25\% \);
d) \(0,5 - \left( {50\% - \frac{3}{5}x} \right) = 2\frac{1}{2}\)
Tìm x biết
a) x : 2,2 = (28,7 – 13,5).2;
b) \(\frac{1}{2}x + \frac{2}{3}(x - 1) = \frac{1}{3}\);
c) \(\frac{2}{3}x:\frac{1}{5} = 1\frac{1}{3}:25\% \);
d) \(0,5 - \left( {50\% - \frac{3}{5}x} \right) = 2\frac{1}{2}\)
Câu 4:
Trong hộp có một số bút xanh và một số bút đỏ, Minh lấy ngẫu nhiên 1 bút từ hộp, xem màu rồi trả lại. Lặp lại hoạt động trên một số lần, Minh được kết quả theo bảng sau:
Loại bút
Bút xanh
Bút đỏ
Số lần
39
11
a) Minh đã thực hiện bao nhiêu lần lấy ngẫu nhiên một chiếc bút từ hộp đó? Bút nào xuất hiện nhiều hơn?
b) Hãy tìm xác suất của thực nghiệm của các sự kiện lấy được bút xanh.
c) Em hãy dự đoán xem trong hộp loại bút nào nhiều hơn .
Trong hộp có một số bút xanh và một số bút đỏ, Minh lấy ngẫu nhiên 1 bút từ hộp, xem màu rồi trả lại. Lặp lại hoạt động trên một số lần, Minh được kết quả theo bảng sau:
|
Loại bút |
Bút xanh |
Bút đỏ |
|
Số lần |
39 |
11 |
a) Minh đã thực hiện bao nhiêu lần lấy ngẫu nhiên một chiếc bút từ hộp đó? Bút nào xuất hiện nhiều hơn?
b) Hãy tìm xác suất của thực nghiệm của các sự kiện lấy được bút xanh.
c) Em hãy dự đoán xem trong hộp loại bút nào nhiều hơn .
Câu 5:
Thực hiện phép tính (tính hợp lí nếu có thể):
a) \(\frac{2}{{11}} - \frac{3}{8} + \frac{4}{{11}} - \frac{6}{{11}} - \frac{5}{8}\);
b) ;
c) (15,25 + 3,75).4 + (20,71 + 5,29).5;
d) \[\left( {4 - \frac{{12}}{{10}}} \right):2 + 30\% \]
Thực hiện phép tính (tính hợp lí nếu có thể):
a) \(\frac{2}{{11}} - \frac{3}{8} + \frac{4}{{11}} - \frac{6}{{11}} - \frac{5}{8}\);
b) ;
c) (15,25 + 3,75).4 + (20,71 + 5,29).5;
d) \[\left( {4 - \frac{{12}}{{10}}} \right):2 + 30\% \]