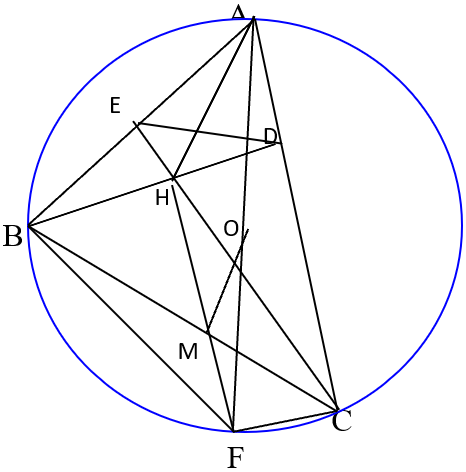
c. Gọi M là trung điểm của BC, chứng minh AH = 2OM
c. Gọi M là trung điểm của BC, chứng minh AH = 2OM
c. Vẽ đường kính AF của đường tròn tâm O ta có ACF = ABF = 90o (góc nội tiếp chắn nữa đường tròn tròn).
Suy ra BH//CF ( vì cùng vuông góc AC ) và CH // BF ( vì cùng vuông góc với AB ) Do đó tứ giác BHCF là hình bình hành
Trong hình bình hành BHCF có M là trung điểm của đường chéo BC nên 3 điểm H, M, F thẳng hàng và M cũng là trung điểm của HF
Trong tam giác AFH có OA = OF ( bán kính) và MH = MF do đó OM là đường trung bình suy ra Om = ½ AH hay AH = 2OM