Bài toán tháp Hà Nội. Bài toán Tháp Hà Nội được được trình bày dưới dạng trò chơi như sau

Bài toán trang 20 Chuyên đề Tin học 11: Bài toán tháp Hà Nội.

Bài toán Tháp Hà Nội được được trình bày dưới dạng trò chơi như sau: Có ba cọc A, B, C. Trên cọc A có một chồng đĩa gồm n cái đĩa, đường kính giảm dần từ dưới lên trên. Cần phải chuyển chồng đĩa từ cọc A sang cọc C tuân thủ quy tắc:

1. Mỗi lần chỉ chuyển một đĩa ở trên cùng của một cọc

2. Chỉ được xếp đĩa có đường kính nhỏ hơn lên trên đĩa có đường kình lớn hơn. Trong quá trình chuyển được phép dùng cột B làm cọc trung gian.

Bài toán đặt ra là: Tìm cách chơi và đưa ra từng bước di chuyển đĩa thoả mãn yêu cầu.

Trả lời

Các Hình 1,2,3 lần lượt minh hoạ các bước di chuyển đĩa cần thực hiện khi số đĩa n = 1,2,3.

Với n = 1: Ta chỉ cần duy nhất một bước di chuyển đĩa từ cọc A sang cọc C.

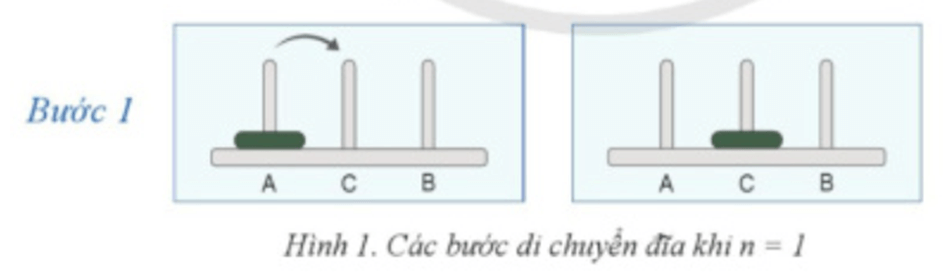
Với n = 2: Ta cần 3 bước di chuyển đĩa.

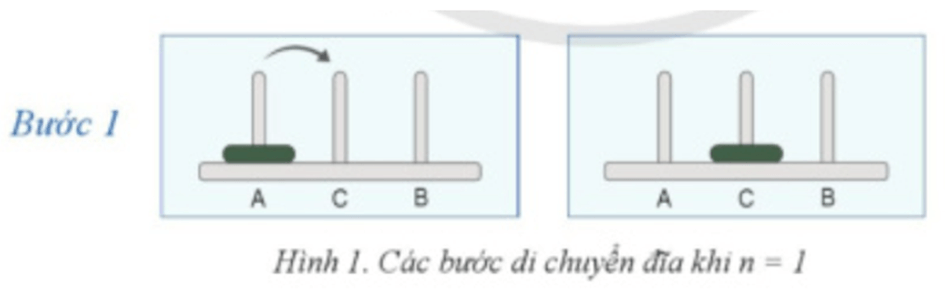
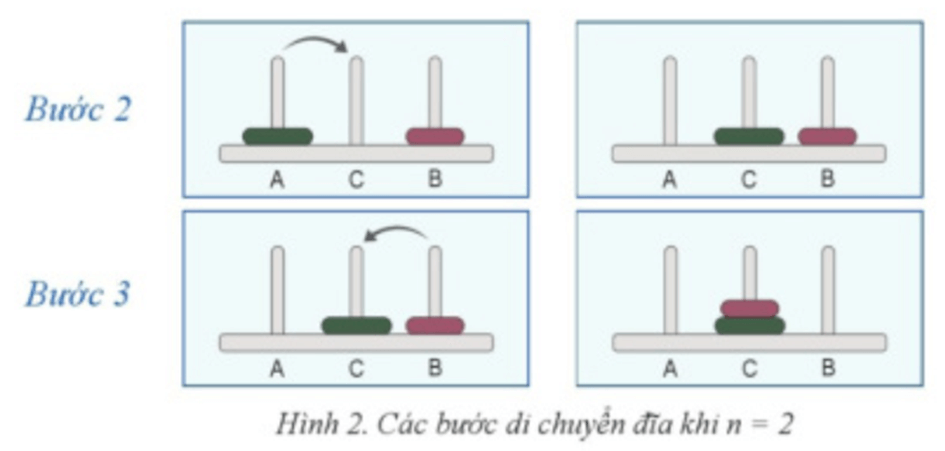
Với n = 3: Ta cần 7 bước di chuyển đĩa

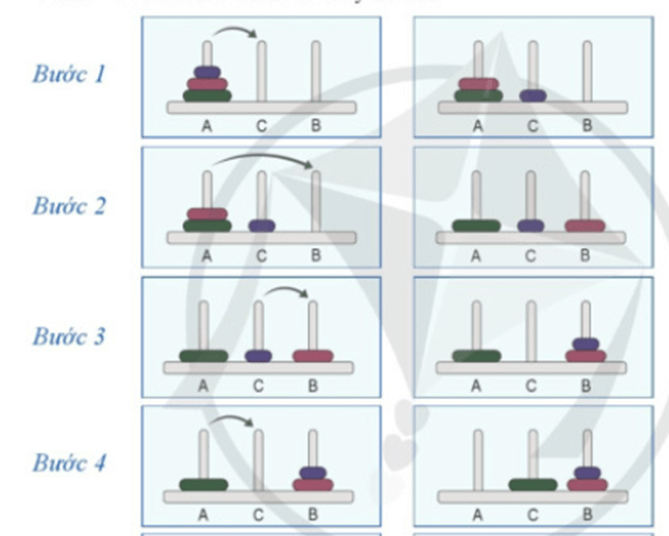
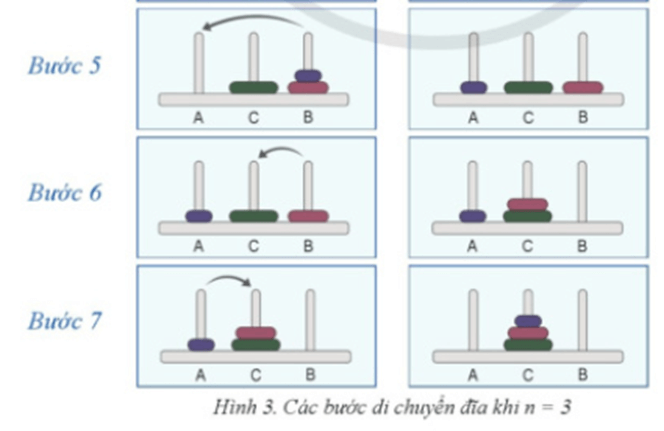
a) Trong quá trình di chuyển đĩa gồm 7 bước với n=3, nhận thấy bài toán Tháp Hà Nội cho trường hợp n=2 được giải hai lần: lần giải đầu tiên bởi ba bước 1, 2, 3 và lần giải thứ hai bởi ba bước 5, 6, 7. Sau ba bước 1, 2, 3 hai đĩa trên cùng của cọc A được chuyển sang cọc B. Do đó, ở lần giải đầu tiên này, cọc A được gọi là cọc xuất phát, cọc B được gọi là cọc đích. Em hãy nêu tên cọc xuất phát và cọc đích ở lần giải thứ hai tương ứng với ba bước 5, 6, 7.

b) Với n = 4, giả sử đã chuyển được ba đĩa trên cùng của cọc A sang cọc B. Em hãy thực hiện tiếp các bước để cả 4 đĩa đều ở cọc C và cho biết khi giải bài toán Tháp Hà Nội với n = 4 ta cần giải bao nhiêu lần bài toán này với n = 3. c) Xây dựng thuật toán đệ quy giải quyết bài toán Tháp Hà Nội với n đĩa và cài đặt thuật toán đề xuất bằng một hàm đệ quy.

d) Viết chương trình yêu cầu người dùng nhập vào số lượng đĩa n và gọi hàm đệ quy đã xây dựng được, để hướng dẫn người chơi các bước di chuyển đĩa. Sau đó, em hãy chạy thử chương trình với các giá trị n lần lượt là 3, 4, 5 để kiểm thử chương trình.

Xem thêm lời giải bài tập Chuyên đề học tập Tin học lớp 11 Cánh diều hay, chi tiết khác:

Bài 2: Thuật toán đệ quy

Bài 3: Thực hành thiết kế thuật toán đệ quy

Bài 4: Thực hành tổng hợp thiết kế thuật toán đệ quy

Bài 1: Ý tưởng chia để trị

Bài 2: Kĩ thuật đệ quy trong chia để trị

Bài 3: Thực hành ứng dụng thuật toán tìm kiếm nhị phân bằng đệ quy