90 Bài tập tích vô hướng của hai vectơ (có đáp án năm 2024) - Toán 10

Tích vô hướng của hai vectơ

Kiến thức cần nhớ

1. Góc giữa hai vectơ

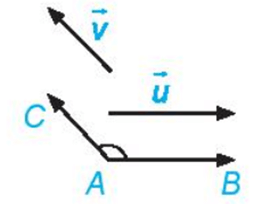
Cho hai vectơ $\overrightarrow{u}$ và $\overrightarrow{v}$ khác $\overrightarrow{0}$. Từ một điểm A tùy ý, vẽ các vectơ $\overrightarrow{AB}=\overrightarrow{u}$ và $\overrightarrow{AC}=\overrightarrow{v}$. Khi đó, số đo của góc BAC được gọi là số đo góc giữa hai vectơ $\overrightarrow{u}$ và $\overrightarrow{v}$ hay đơn giản là góc giữa hai vectơ $\overrightarrow{u}$, $\overrightarrow{v}$, kí hiệu là ($\overrightarrow{u}$, $\overrightarrow{v}$).

Chú ý :

+ Quy ước rằng góc giữa hai vectơ $\overrightarrow{u}$ và $\overrightarrow{0}$ có thể nhận một giá trị tùy ý từ 0° đến 180°.

+ Nếu ($\overrightarrow{u}$, $\overrightarrow{v}$) = 90° thì ta nói rằng $\overrightarrow{u}$ và $\overrightarrow{v}$ vuông góc với nhau. Kí hiệu $\overrightarrow{u}$ ⊥ $\overrightarrow{v}$ hoặc $\overrightarrow{v}$ ⊥ $\overrightarrow{u}$. Đặc biệt được coi là vuông góc với mọi vectơ.

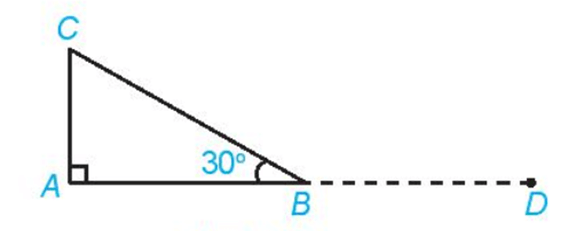
Ví dụ: Cho tam giác ABC vuông tại A và $\hat{B}=30°$. Tính $(\overrightarrow{AB},\overrightarrow{AC})$, $(\overrightarrow{CA},\overrightarrow{CB})$, $(\overrightarrow{AB},\overrightarrow{BC})$.

Hướng dẫn giải

Ta có $(\overrightarrow{AB},\overrightarrow{AC})$ = $\widehat{BAC}=90°$.

Tam giác ABC vuông tại A nên ta có .

$\widehat{ACB}+\widehat{ABC}=90°\Rightarrow \widehat{ACB}=90°-\widehat{ABC}=90°-30°=60°$

Suy ra: $(\overrightarrow{CA},\overrightarrow{CB})=\widehat{ACB}=60°$.

Vẽ $\overrightarrow{BD}$ sao cho $\overrightarrow{BD}$ = $\overrightarrow{AB}$. Khi đó $(\overrightarrow{AB},\overrightarrow{BC})$ = $(\overrightarrow{BD},\overrightarrow{BC})$ = $\widehat{CBD}$.

Mặt khác $\widehat{ABC}+\widehat{CBD}=180°$ (hai góc kề bù)

Suy ra $\widehat{CBD}=180°-\widehat{ABC}=180°-30°=150°$.

Do đó, $(\overrightarrow{AB},\overrightarrow{BC})$ = $\widehat{CBD}$ = 150°.

Vậy $(\overrightarrow{AB},\overrightarrow{AC})$ = 90°, $(\overrightarrow{CA},\overrightarrow{CB})$ = 60°, $(\overrightarrow{AB},\overrightarrow{BC})$ = 150°.

2. Tích vô hướng của hai vectơ

Tích vô hướng của hai vectơ khác vectơ-không $\overrightarrow{u}$ và $\overrightarrow{v}$ là một số, kí hiệu là $\overrightarrow{u}$.$\overrightarrow{v}$, được xác định bởi công thức sau:

$\overrightarrow{u}$. $\overrightarrow{v}$ = |$\overrightarrow{u}$|.|$\overrightarrow{v}$|.cos($\overrightarrow{u}$, $\overrightarrow{v}$)

Chú ý:

+) $\overrightarrow{u}$ ⊥ $\overrightarrow{v}$ ⇔ $\overrightarrow{u}$. $\overrightarrow{v}$ = 0.

+) $\overrightarrow{u}$. $\overrightarrow{u}$ còn được viết là ${\overrightarrow{u}}^2$ và được gọi là bình phương vô hướng của vectơ $\overrightarrow{u}$.

Ta có ${\overrightarrow{u}}^2=\left|\overrightarrow{u}\right|.\left|\overrightarrow{u}\right|.\cos 0°={\left(\overrightarrow{u}\right)}^2$.

(Bình phương vô hướng của một vectơ bằng bình phương độ dài của vectơ đó.)

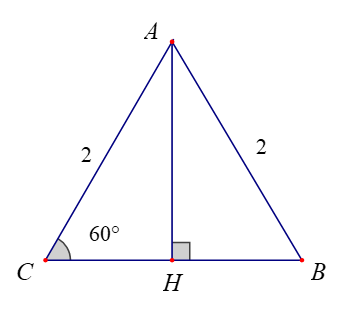
Ví dụ: Cho tam giác đều ABC có cạnh bằng 2 và có đường cao AH. Tính các tích vô hướng:

a) $\overrightarrow{AB}.\overrightarrow{AC}$;

b) $\overrightarrow{AH}.\overrightarrow{BC}$.

Hướng dẫn giải

a) Vì tam giác ABC đều nên $(\overrightarrow{AB},\overrightarrow{AC})=\widehat{BAC}=60°$.

Suy ra: $\overrightarrow{AB}.\overrightarrow{AC}=\left|\overrightarrow{AB}\right|.\left|\overrightarrow{AC}\right|\cos (\overrightarrow{AB},\overrightarrow{AC})=\mathrm{2.2.}\cos 60°=\mathrm{2.2.}\frac{1}{2}=2$.

Vậy $\overrightarrow{AB}.\overrightarrow{AC}$ = 2.

b) Vì AH là đường cao của tam giác ABC nên AH ⊥ BC.

Do đó $(\overrightarrow{AH},\overrightarrow{BC})=90°$.

Ta có: $\overrightarrow{AH}.\overrightarrow{BC}=\left|\overrightarrow{AH}\right|.\left|\overrightarrow{BC}\right|\cos (\overrightarrow{AH},\overrightarrow{BC})=\left|\overrightarrow{AH}\right|.\left|\overrightarrow{BC}\right|\cos 90°=\left|\overrightarrow{AH}\right|.\left|\overrightarrow{BC}\right|.0=0$.

Vậy $\overrightarrow{AH}.\overrightarrow{BC}$ = 0.

3. Biểu thức tọa độ và tính chất của tích vô hướng

• Tích vô hướng của hai vectơ $\overrightarrow{u}=(x;y)$ và $\overrightarrow{v}=(x\text{'};y\text{'})$ được tính theo công thức :

$\overrightarrow{u}$. $\overrightarrow{v}$ = x.x' + y.y'.

Nhận xét:

+ Hai vectơ $\overrightarrow{u}$ và $\overrightarrow{v}$ vuông góc với nhau khi và chỉ khi x.x' + y.y' = 0.

+ Bình phương vô hướng của $\overrightarrow{u}=(x;y)$ là ${\overrightarrow{u}}^2$ = x² + y².

+ Nếu $\overrightarrow{u}$ ≠ $\overrightarrow{0}$ và $\overrightarrow{v}$ ≠ $\overrightarrow{0}$ thì cos($\overrightarrow{u}$, $\overrightarrow{v}$) = $\frac{\overrightarrow{u}.\overrightarrow{v}}{\left|\overrightarrow{u}\right|.\left|\overrightarrow{v}\right|}=\frac{xx\text{'}+yy\text{'}}{\sqrt{x^2+y^2}.\sqrt{x{\text{'}}^2+y{\text{'}}^2}}$.

Ví dụ: Trong mặt phẳng tọa độ cho hai vectơ $\overrightarrow{u}=(0;-5)$ và $\overrightarrow{v}=(\sqrt{3};1)$ .

a) Tính tích vô hướng của hai vectơ trên.

b) Tìm góc giữa của hai vectơ trên.

Hướng dẫn giải

a) Ta có: $\overrightarrow{u}$. $\overrightarrow{v}$ = 0.$\sqrt{3}$ + (–5).1= –5;

Vậy $\overrightarrow{u}$. $\overrightarrow{v}$ = –5.

b) Ta có $|\overrightarrow{u|}=\sqrt{0^2+{(-5)}^2}=5$; $\left|\overrightarrow{v}\right|=\sqrt{{\left(\sqrt{3}\right)}^2+1^2}=2$

Suy ra : cos($\overrightarrow{u}$, $\overrightarrow{v}$) = $\frac{\overrightarrow{u}.\overrightarrow{v}}{\left|\overrightarrow{u}\right|.\left|\overrightarrow{v}\right|}=\frac{-5}{5.2}=\frac{-5}{10}=\frac{-1}{2}$.

Suy ra ($\overrightarrow{u}$, $\overrightarrow{v}$) = 120°.

Vậy ($\overrightarrow{u}$, $\overrightarrow{v}$) = 120°.

• Tính chất của tích vô hướng :

Với ba vectơ $\overrightarrow{u}$, $\overrightarrow{v}$, $\overrightarrow{\text{w}}$ bất kì và mọi số thực k, ta có :

+) $\overrightarrow{u}$. $\overrightarrow{v}$ = $\overrightarrow{v}$. $\overrightarrow{u}$ (tính chất giao hoán);

+) $\overrightarrow{u}$. ($\overrightarrow{v}$ + $\overrightarrow{\text{w}}$) = $\overrightarrow{u}$. $\overrightarrow{v}$ + $\overrightarrow{u}$. $\overrightarrow{\text{w}}$ (tính chất phân phối đối với phép cộng) ;

+) (k $\overrightarrow{u}$). $\overrightarrow{v}$ = k ($\overrightarrow{u}$. $\overrightarrow{v}$) = $\overrightarrow{u}$.( k$\overrightarrow{v}$).

Chú ý: Từ tính trên, ta có thể chứng minh được :

$\overrightarrow{u}$. ($\overrightarrow{v}$ – $\overrightarrow{\text{w}}$)= $\overrightarrow{u}$. $\overrightarrow{v}$ – $\overrightarrow{u}$. $\overrightarrow{\text{w}}$ (tính chất phân phối đối với phép trừ) ;

($\overrightarrow{u}$ + $\overrightarrow{v}$)² = ${\overrightarrow{u}}^2$ + 2$\overrightarrow{u}$. $\overrightarrow{v}$ + ${\overrightarrow{v}}^2$; ($\overrightarrow{u}$ – $\overrightarrow{v}$)² = ${\overrightarrow{u}}^2$ –2$\overrightarrow{u}$.$\overrightarrow{v}$ + ${\overrightarrow{v}}^2$;

($\overrightarrow{u}$ + $\overrightarrow{v}$).($\overrightarrow{u}$ – $\overrightarrow{v}$) = ${\overrightarrow{u}}^2$ – ${\overrightarrow{v}}^2$.

Ví dụ: Cho tam giác ABC. Chứng minh rằng với điểm M tùy ý ta có:

$\overrightarrow{MA}.\overrightarrow{BC}+\overrightarrow{MB}.\overrightarrow{CA}+\overrightarrow{MC}.\overrightarrow{AB}=0$.

Hướng dẫn giải

Ta có $\overrightarrow{MA}.\overrightarrow{BC}=\overrightarrow{MA}.(\overrightarrow{MC}-\overrightarrow{MB})=\overrightarrow{MA}.\overrightarrow{MC}-\overrightarrow{MA}.\overrightarrow{MB};$(1)

$\overrightarrow{MB}.\overrightarrow{CA}=\overrightarrow{MB}.(\overrightarrow{MA}-\overrightarrow{MC})=\overrightarrow{MB}.\overrightarrow{MA}-\overrightarrow{MB}.\overrightarrow{MC};$ (2)

$\overrightarrow{MC}.\overrightarrow{AB}=\overrightarrow{MC}.(\overrightarrow{MB}-\overrightarrow{MA})=\overrightarrow{MC}.\overrightarrow{MB}-\overrightarrow{MC}.\overrightarrow{MA}$. (3)

Cộng các kết quả từ (1), (2), (3), ta được: $\overrightarrow{MA}.\overrightarrow{BC}+\overrightarrow{MB}.\overrightarrow{CA}+\overrightarrow{MC}.\overrightarrow{AB}=0$

Vậy $\overrightarrow{MA}.\overrightarrow{BC}+\overrightarrow{MB}.\overrightarrow{CA}+\overrightarrow{MC}.\overrightarrow{AB}=0$.

Các dạng bài tập tích vô hướng của hai vectơ

Dạng 1. Xác định góc giữa hai vectơ.

+ Sử dụng nghĩa góc giữa hai vectơ.

+ Sử dụng tính chất của tam giác, hình vuông.

Dạng 2. Tích vô hướng của hai vectơ.

+ Dựa vào nghĩa a.b = |a|.|B|.cos(a;b).

+ Sử dụng tính chất và các hằng đẳng thức của tích vô hướng của hai vectơ.

Dạng 3. Chứng minh các đẳng thức về tích vô hướng hoặc độ dài.

+ Nếu trong đẳng thức chứa bình phương độ dài của đoạn thẳng thì ta chuyển về vectơ nhờ đẳng thức AB2 = AB2.

+ Sử dụng các tính chất của tích vô hướng, các quy tắc phép toán vectơ.

+ Sử dụng hằng đẳng thức vectơ về tích vô hướng.

Dạng 4. Điều kiện vuông góc.

+ Cho a = (x1;y1) và b = (x2;y2). Khi đó a vuông góc b khi và chỉ khi a.b = 0 khi và chỉ khi x1.x2 + y1.y2 = 0.

Dạng 5. Các bài toán tìm tập hợp điểm.

+ Ta sử dụng các kết quả cơ bản sau: Cho A, B là các điểm cố định và M là điểm di động:

- Nếu |AM| = k với k là số thực dương cho trước thì tập hợp các điểm M là đường tròn tâm A, bán kính R = k.

- Nếu MA.MB = 0 thì tập hợp các điểm M là đường tròn đường kính AB.

- Nếu MA.a = 0 với a khác 0 cho trước thì tập hợp các điểm M là đường thẳng đi qua A và vuông góc với giá của vectơ a.

Dạng 6. Cực trị.

+ Sử dụng kiến thức tổng hợp để giải toán.

Bài tập tự luyện

1. Bài tập vận dụng

B1. Bài tập trắc nghiệm

Câu 1. Trong mặt phẳng tọa độ, cặp vectơ nào sau đây vuông góc với nhau?

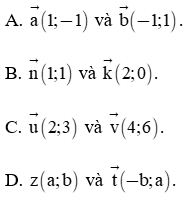
Hướng dẫn giải

Đáp án đúng là D

Ta có: $\overrightarrow{a}.\overrightarrow{b}=1.\left(-1\right)+\left(-1\right).1=-1+\left(-1\right)=-2\ne 0.$  Suy ra hai vecto $\overrightarrow{a},\overrightarrow{b}$  không vuông góc với nhau. Do đó A sai.

Ta có: $\overrightarrow{n}.\overrightarrow{k}=1.2+1.0=2+0=2\ne 0.$  Suy ra hai vecto $\overrightarrow{n},\overrightarrow{k}$  không vuông góc. Do đó B sai.

Ta có: $\overrightarrow{u}.\overrightarrow{v}=2.4+3.6=8+18=26\ne 0.$  Suy ra hai vecto $\overrightarrow{u},\overrightarrow{v}$  không vuông góc. Do đó C sai.

Ta có: $\overrightarrow{z}.\overrightarrow{t}=a.\left(-b\right)+b.a=-ab+ab=0.$  Suy ra hai vecto $\overrightarrow{z},\overrightarrow{t}$  vuông góc với nhau. Do đó D đúng.

Câu 2. Góc giữa vectơ $\overrightarrow{a}\left(-1;-1\right)$  và vecto $\overrightarrow{b}\left(-1;0\right)$  có số đo bằng:

A. 90°.

B. 0°.

C. 135°.

D. 45°.

Hướng dẫn giải

Đáp án đúng là D

Ta có: $\overrightarrow{a}.\overrightarrow{b}=\left(-1\right).\left(-1\right)+\left(-1\right).0=1,$ $\left|\overrightarrow{a}\right|=\sqrt{{\left(-1\right)}^2+{\left(-1\right)}^2}=\sqrt{2},$ $\left|\overrightarrow{b}\right|=\sqrt{{\left(-1\right)}^2+0^2}=1.$

$\Rightarrow cos\left(\overrightarrow{a}.\overrightarrow{b}\right)=\frac{\overrightarrow{a}.\overrightarrow{b}}{\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|}=\frac{1}{\sqrt{2}}\Rightarrow \left(\overrightarrow{a}.\overrightarrow{b}\right)=45°.$

Vậy góc giữa hai vec tơ $\overrightarrow{a}$  và $\overrightarrow{b}$ là 45°.

Câu 3. Cho hình vuông ABCD có độ dài cạnh là a và A(0; 0), B(a; 0), C(a; a), D(0; a). Khẳng định nào sau đây là đúng?

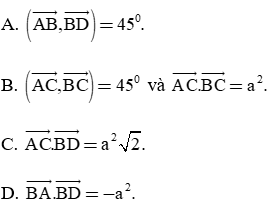
Hướng dẫn giải

Đáp án đúng là B

Vì ABCD là hình vuông cạnh a nên AB = BC = a, BD = AC = a$\sqrt{2}$ .

B2. Bài tập tự luận

Câu 4: Cho hai vectơ $\overrightarrow{a}=(1;-2);\overrightarrow{b}=(-1;-3)$.

a) Tính tích vô hướng của $\overrightarrow{a}$ và $\overrightarrow{b}$.

b) Tính góc giữa hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ .

Hướng dẫn giải

a) Ta có $\overrightarrow{a}$ .$\overrightarrow{b}$ = 1.(–1) + (–2).(–3) = 5.

Vậy $\overrightarrow{a}$ . $\overrightarrow{b}$ = 5.

b) Ta có $\left|\overrightarrow{a}\right|=\sqrt{1^2+{(-2)}^2}=\sqrt{5}$; $\left|\overrightarrow{b}\right|=\sqrt{{(-1)}^2+{(-3)}^2}=\sqrt{10}$.

Khi đó cos($\overrightarrow{a}$, $\overrightarrow{b}$) = $\frac{\overrightarrow{a}.\overrightarrow{b}}{\left|\overrightarrow{a}\right|.\left|\overrightarrow{b}\right|}=\frac{5}{\sqrt{5}.\sqrt{10}}=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}$.

Suy ra ($\overrightarrow{a}$, $\overrightarrow{b}$ ) = 45°.

Vậy góc giữa hai vectơ và là 45°.

Câu 5: Trong mặt phẳng tọa độ Oxy cho hai điểm A(2; 4) và B(1; 1). Tìm tọa độ của điểm C sao cho tam giác ABC là tam giác vuông cân tại B.

Hướng dẫn giải

Giả sử điểm C cần tìm có tọa độ (x; y). Để tam giác ABC vuông cân tại B ta phải có:

$\left(\begin{array}{c}\overrightarrow{BA}.\overrightarrow{BC}=0\\ \left|\overrightarrow{BA}\right|=\left|\overrightarrow{BC}\right|\end{array}\right)$

Ta có $\overrightarrow{BA}=(1;3)$ và $\overrightarrow{BC}=(x-1;y-1)$.

Khi đó $\overrightarrow{BA}.\overrightarrow{BC}=1.(x-1)+3(y-1)=x+3y-4$.

Và $\left|\overrightarrow{BA}\right|=\sqrt{1^2+3^2}=\sqrt{10}$; $\left|\overrightarrow{BC}\right|=\sqrt{{(x-1)}^2+{(y-1)}^2}$

Ta có: $\left(\begin{array}{c}\overrightarrow{BA}.\overrightarrow{BC}=0\\ \left|\overrightarrow{BA}\right|=\left|\overrightarrow{BC}\right|\end{array}\right)$

⇔ $\left(\begin{array}{c}x+3y-4=0\\ \sqrt{10}=\sqrt{{(x-1)}^2+{(y-1)}^2}\end{array}\right)$

⇔ $\left(\begin{array}{c}x+3y-4=0\\ \sqrt{10}=\sqrt{{(x-1)}^2+{(y-1)}^2}\end{array}\right)$

⇔ $\left(\begin{array}{c}x+3y-4=0\\ 10={(x-1)}^2+{(y-1)}^2\end{array}\right)$

⇔ $\left(\begin{array}{c}x=4-3y\\ {(3-3y)}^2+{(y-1)}^2=10\end{array}\right)\iff \left(\begin{array}{c}x=4-3y\\ 10y^2-20y=0\end{array}\right)$

⇔ $\left(\begin{array}{c}x=4-3y\\ \left(\begin{array}{c}y=0\\ y=2\end{array}\right)\end{array}\right)$ ⇔ $\left(\begin{array}{c}\left(\begin{array}{c}x=4\\ y=0\end{array}\right)\\ \left(\begin{array}{c}x=-2\\ y=2\end{array}\right)\end{array}\right)$

Vậy có hai điểm C và C’ thỏa mãn điều kiện của bài toán: C(4; 0) và C’(–2; 2).

2. Bài tập tự luyện có hướng dẫn

Xem thêm các dạng bài tập liên quan khác:

90 Bài tập tích vô hướng của hai vectơ (có đáp án năm 2023)

80 Bài tập số gần đúng và sai số (có đáp án năm 2023)

80 Bài tập về Tích vô hướng của một vectơ với một số (có đáp án năm 2023)

80 Bài tập Tổng và hiệu của hai vectơ (có đáp án năm 2023)

90 Bài tập các khái niệm mở đầu (có đáp án năm 2023)