80 bài tập về chia đa thức một biến đã sắp xếp (có đáp án năm 2023) - Toán 8

Bài giảng Toán 8 Bài 12: Chia đa thức một biến đã sắp xếp

Lý thuyết

1. Phép chia hết

- Phép chia hết là phép chia có đa thức dư bằng 0.

Quy tắc chia:

+ Sắp xếp các đa thức theo thứ tự giảm dần của biến.

+ Lấy hạng tử cao nhất của đa thức bị chia chia cho hạng tử cao nhất của đa thức chia ta được thương 1.

+ Nhân thương 1 với đa thức chia và lấy đa thức bị chia trừ đi tích đó.

+ Lấy hạng tử cao nhất của đa thức vừa tìm được chia cho hạng tử cao nhất đa thức chia ta được thương 2.

+ Tiếp tục lặp lại các bước trên đến khi nhận được hiệu bằng 0.

Ví dụ 1: Làm tính chia: (x³ – x²  – 5x – 3) : (x – 3).

Lời giải:

Ta có:

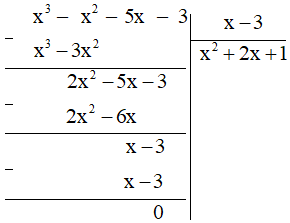
Vậy (x³ – x² – 5x – 3) : (x – 3) = x² + 2x + 1.

2. Phép chia có dư

- Phép chia có dư là phép chia có đa thức dư khác 0.

Quy tắc chia: Làm tương tự phép chia hết đến khi thu được đa thức dư có bậc nhỏ hơn bậc của đa thức chia.

Chú ý: Với hai đa thức tùy ý A và B của cùng một biến (B ≠ 0), tồn tại duy nhất một cặp đa thức Q và R sao cho A = B.Q + R, trong đó R = 0 hoặc bậc của R nhỏ hơn bậc của B (R được gọi là dư trong phép chia A cho B).

Khi R = 0 phép chia A cho B là phép chia hết.

Ví dụ 2: Làm tính chia: (3x³ + 2x² + 5x – 3) : (x² + 1).

Lời giải:

Ta có:

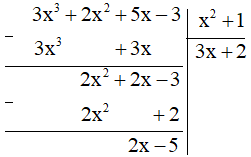
Vậy (3x³ + 2x² + 5x – 3) : (x² + 1) = 3x + 2 (dư 2x – 5)

Hay 3x³ + 2x² + 5x – 3 = (x² + 1).(3x + 2) + 2x – 5.

Các dạng bài tập về chia đa thức một biến đã sắp xếp

Dạng 1: Sử dụng hằng đẳng thức để thực hiện phép chia đa thức

1. Phương pháp giải

Có thể dùng các hằng đẳng thức đấng nhớ sau để rút gọn phép chia đa thức:

$\begin{array}{l}(A^3+B^3):(A+B)=A^2-AB+B^2\\ (A^3-B^3):(A-B)=A^2+AB+B^2\\ (A^2-B^2):(A+B)=A-B\end{array}$

2. Bài tập minh hoạ

Ví dụ 1: Áp dụng hẳng đẳng thức đáng nhớ để thực hiện các phép chia sau:

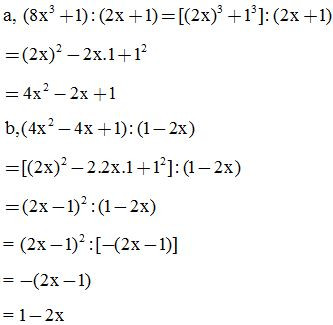
Ví dụ 2: Áp dụng hằng đẳng thức đáng nhớ để thực hiện phép chia:

Hướng dẫn giải

Hoặc 

Ví dụ 3: Thực hiện phép chia đa thức  cho đa thức .

Hướng dẫn giải

Lưu ý rằng: nếu chia cho đa thức  thì , còn nếu chia cho đa thức  thì 

Dựa vào hướng dẫn trên ta sẽ có sơ đồ Hoocne như sau:

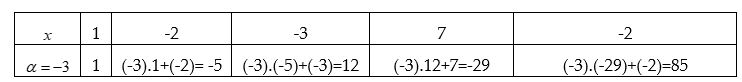
Đa thức  tìm được ở đây chính là:

và 

Vậy khi chia đa thức  cho đa thức  ta được:

* Tuy nhiên không phải lúc nào bài toán cũng yêu cầu thực hiện phép chia đa thức bằng sơ đồ Hoocne. Vậy thì trong một số trường hợp sau đây ta có thể sử dụng sơ đồ:

+ Chia đa thức cho đa thức một cách nhanh nhất.

+ Tìm nghiệm của phương trình bậc 3, phương trình bậc 4, phương trình bậc cao.

+ Phân tích đa thức thành nhân tử (với những đa thức có bậc lớn hơn 2).

Dạng 2: Tìm thương và số dư trong phép chia đa thức

1. Phương pháp giải

Từ điều kiện đề bài đã cho, đặt phép chia A cho B rồi viết A dưới dạng A =  B.Q + R

2. Bài tập minh họa

Ví dụ 1:

a, Cho hai đa thức A = $x^3-x^2-5x-3$ và B = $x-3$. Tìm dư R trong phép chia A cho B và viết A dưới dạng A = B.Q + R

b, Cho đa thức A = $3x^4+x^3+6x-5$ và B = $x^2+1$. Tìm dư R trong phép chia A cho B và viết A dưới dạng A = B.Q + R

Hướng dẫn giải

a, Ta thực hiện phép chia sau:

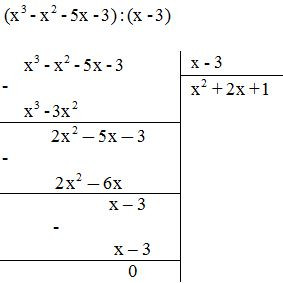
KL:

- Vậy số dư trong phép chia là 0

A = (x - 3).($x^2+2x+1$) + 0

b, Ta thực hiện phép chia sau:

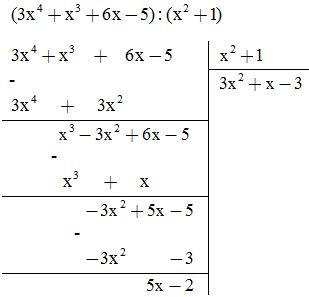
KL:

- Vậy số dư trong phép chia là 5x – 2

A = ($x^2+1$).($3x^2+x-3$) + (5x – 2)

Dạng 3: Tìm điều kiện để thực hiện phép chia đa thức

1. Phương pháp giải:

* Thực hiện phép chia A : B để tìm biểu thức dư R theo m

Để A chia hết cho B thì R = 0$\Rightarrow$m

* Tìm số nguyên n để A chia hết cho B (với A , B là các biểu thức theo n)

- Thực hiện A : B tìm số dư là số nguyên k, thương là biểu thức Q

- Viết A = Q.B + k

- Để A chia hết cho B$\iff$k chia hết cho B$\iff$B là Ư(k)$\Rightarrow$n

2. Ví dụ minh họa:

VD1: Tìm k để $f\left(x\right)=x^4-9x^3+21x^2+x+k$ chia hết cho g(x) = x – 2

Giải: Ta thực hiện phép chia sau:

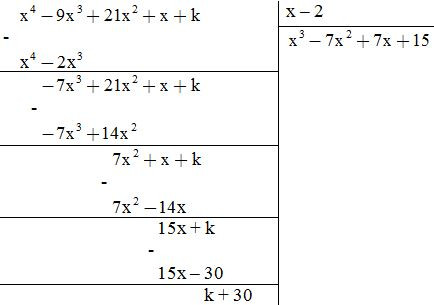
Để f(x) chia hết cho g(x) thì k + 30 = 0$\iff$k = - 30.

KL: Vậy với k = -30 thì f(x) chia hết cho g(x)

VD2: Tìm số nguyên x để đa thức A = 8x² - 4x +1 chia hết cho đa thức B = 2x + 1

Giải: Ta thực hiện phép chia sau:

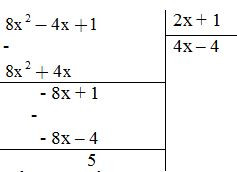
Để A chia hết cho B thì 5 (2x + 1)$\iff$ (2x + 1)$\in$Ư(5)

KL: Vậy x = {-3, -1, 0, 2}