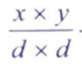Sách bài tập Tin học 11 Bài 4: Làm mịn dần từng bước từ thuật toán đến chương trình máy tính
result 0
for i in li
Isisn):
for / in UiSj≤n):
result result + I
return result
Lời giải:
Kết quả trả về sau cùng là:
result ←0
for i in (il sis vn):
if mii:
result result + 1
if ix in:
result result + 1
return result
Lời giải:
Đoạn mã giả sẽ trả về số lượng ước dương của n. Với nhận xét tương tự như bài toán kiểm tra tính nguyên tố trong sách giáo khoa, ta chỉ cần duyệt đến sqrt(n) để thống kê tất cả các cặp ước số. Ngoài ra, em phải xét riêng trường hợp số chính phương n = i x i
Yêu cầu: Cô giáo cho trước tấm bìa, em hãy xác định số hình vuông ít nhất có thể cắt được.
Dữ liệu: Nhập từ thiết bị vào chuẩn, gồm hai dòng:
• Dòng thứ nhất chứa số nguyên dương x (x<10).
• Dòng thứ hai chứa số nguyên dương y (y<10).
Kết quả: Hiển thị ở thiết bị ra chuẩn số lượng hình vuông theo yêu cầu.
Ví dụ:
Input
15
9
Output
Lời giải:
Để cắt hết tấm bìa mà không còn thừa mảnh nào thì kích thước cạnh d của hình vuông được cắt ra là ước số của x và y (x : d và y : d).
- Số lượng hình vuông ít nhất thì d phải lớn nhất, tức là: d = ƯCLN (x, y).
- Vậy kết quả của bài toán là:
Đầu vào: Hai số nguyên x, y.
Đầu ra: Số lượng hình vuông thoả mãn.
Thuật toán thô: Tìm giá trị max{d | x : d; y : d).
– Lặp khi min(x,y)>d>1:
Nếu phát hiện x chia hết cho d và y chia hết cho d thì kết quả bài toán là:
Cải tiến:
Nhận xét: Giá trị của d chính là ước số chung lớn nhất của x và y, có thể dùng hàm có sẵn tìm ước chung lớn nhất để chương trình chạy nhanh hơn.
Câu Fcs16 trang 50 SBT Tin học 11: Độ đẹp của số nguyên
• Sau khi nghe câu chuyện “Bàn cờ và hạt thóc” (nói về luỹ thừa của 2), Bình cảm thấy toán học thật thú vị nên cũng muốn thử làm nên một “sự tích” như vậy. Cậu lấy y hạt gạo ra và thử xếp chúng thành một hình chữ nhật trên bàn cờ vua, tức là mỗi ô chỉ chứa một hạt gạo và các ô có gạo tạo thành một hình chữ nhật. Bình định nghĩa độ đẹp của số x là số cách khác nhau để xếp c hạt gạo lên bàn cờ vua. Ví dụ, với x = 6 thì độ đẹp là 4 do ta có bốn cách tương ứng với các hình chữ nhật có kích thước là 1 × 6; 2 × 3; 3 × 2; 6 × 1. Tổng quát hơn, có thể coi độ đẹp là một hàm theo x, kí hiệu f(x). Ở đây, ta giả sử bàn cờ luôn đủ lớn (chứ không gói gọn trong kích thước 8 × 8). Ví dụ, với x 11 thì vẫn có thể xếp theo hai cách là 1 × 11 hoặc 11 × 1.
Bình thắc mắc tăng trong n số nguyên dương đầu tiên thì số có độ đẹp lớn nhất là số như Em hãy viết chương trình giúp Bình giải đáp thắc mắc này Dù lựu. Nhập từ thiết bị vào chuẩn một số nguyên dương a.
Acqua Diana thiết bị chuẩn độ đẹp lớn nhất của n số nguyên dương đầu tiên.
Giải thích. Từ 1 đến 17 có số 12 là đẹp nhất. Số 1 kích thước khác nhau là 1× 12, 2014 4 6:3 4:4 × đẹp lớn nhất từ 1 đến 17 là 6.
có ở hình chữ nhật có 3,0 x2 × L. Vậy độ 3; 6 2:12
Lời giải:
f(x) = số lượng ước số của x.
Thuật toán thô
– Tạo hàm ((-x), đếm số lượng ước số của x.
Lặp khi 1 < f(x,) thì gán x = x (x là kết quả bài toán, ban đầu x − 1).
Cải tiến:
Nhận xét: x chia hết cho i nghĩa là x = i × j, x có hai ước là i và j. Giả sử i
Cải tiến hàm f(x) như sau:
Mã giả
Xem thêm các bài giải sách bài tập Tin học lớp 11 Cánh diều hay, chi tiết khác:
Bài 1: Kiểu mảng và cấu trúc mảng
Bài 2, 3: Mảng hai chiều, Thực hành về tệp, mảng và danh sách