15 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 10 CTST Bài tập cuối chương 6 có đáp án (Phần 2) (Thông hiểu)

Câu 1:

Hỏi kết quả đo đạc nào trong các kết quả sau đây là chính xác nhất?

A. 22,34 m ± 0,01 m;

B. 107,2 m ± 0,2 m;

C. 2001,8 m ± 0,5 m;

D. 56,48 m ± 0,12 m;

Xem đáp án

Đáp án đúng là: C

Ta so sánh sai số tương đối của các phép đo:

$δ_{1} = \frac{0,01}{22,34} = 0,00044762...$

$δ_{2} = \frac{0,2}{107,2} = 0,00186567...$

$δ_{3} = \frac{0,5}{2001,8} = 0,0002497752...$

$δ_{2} = \frac{0,12}{56,48} = 0,002124645...$

Ta có δ3 có giá trị nhỏ nhất nên phép đo ở phương án C có kết quả chính xác nhất.

Câu 2:

Trong một cuộc điều tra dân số năm 2022, người ta báo cáo số dân của tỉnh X là ā = 2 718 156 ± 150 người. Số quy tròn của số a = 2 718 156 là:

A. 2 718 000;

B. 2 718 400;

C. 2 718 500;

D. 1 719 000.

Xem đáp án

Đáp án đúng là: A

Hàng lớn nhất của độ chính xác d = 150 là hàng trăm nên ta quy tròn a đến hàng nghìn. Khi đó số quy tròn của a là 2 718 000.

Vậy ta chọn phương án A.

Câu 3:

Cho số gần đúng là a = 1 922 với độ chính xác d = 50. Số quy tròn của số a là:

A. 2 000;

B. 1 950;

C. 1 900;

D. 1 920.

Xem đáp án

Đáp án đúng là: C

Hàng lớn nhất của độ chính xác d = 50 là hàng chục nên ta quy tròn a đến hàng trăm.

Khi đó số quy tròn của a là 1 900.

Vậy ta chọn phương án C.

Câu 4:

Một lớp học có 3 tổ học sinh, khi trồng cây trong buổi ngoại khóa có kết quả như sau:

Tổ	1	2	3
Số học sinh	9	10	9
Số cây	27	31	25

Mỗi bạn học sinh đều không trồng quá 3 cây. Hỏi trong bảng đã thống kê sai tổ nào?

A. Tổ 1;

B. Tổ 2;

C. Tổ 3;

D. Cả 3 tổ.

Xem đáp án

Đáp án đúng là: B

Ta có:

• Số cây tối đa tổ 1 trồng được là: 9 . 3 = 27 (cây).

Do đó đã thống kê đúng số cây của tổ 1.

• Số cây tối đa tổ 2 trồng được là: 10 . 3 = 30 (cây) < 31 (cây).

Do đó đã thống kê sai số cây của tổ 2.

• Số cây tối đa tổ 3 trồng được là: 9 . 3 = 27 (cây) > 25 (cây).

Do đó đã thống kê đúng số cây của tổ 3.

Vậy tổ 2 thống kê sai kết quả.

Câu 5:

Người ta thống kê ước tính tốc độ tăng kim ngạch xuất, nhập khẩu hàng hóa 2 tháng đầu năm giao đoạn 2018 – 2022 (%) như sau:

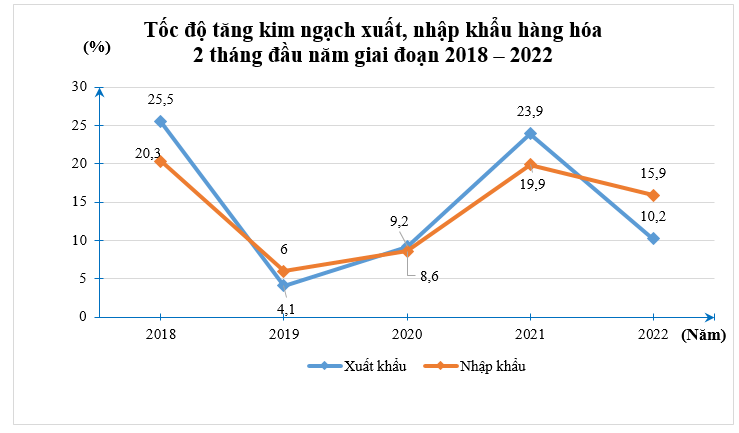
Người ta thống kê ước tính tốc độ tăng kim ngạch xuất, nhập khẩu hàng hóa 2 tháng đầu (ảnh 1)

So với năm 2020 thì năm 2022 kim ngạch xuất khẩu tăng hay giảm bao nhiêu %?

A. Tăng 7,3%;

B. Giảm 1%;

C. Tăng 1%;

D. Tăng 5,1%;

Xem đáp án

Đáp án đúng là: C

Quan sát biểu đồ, ta thấy:

Năm 2022 kim ngạch xuất khẩu của nước ta là: 10,2%.

Năm 2020, kim ngạch xuất khẩu của nước ta là: 9,2%.

Do đó so với năm 2020 thì năm 2022 kim ngạch xuất khẩu tăng 10,2% ‒ 9,2% = 1%.

Câu 6:

Biểu đồ dưới đây thể hiện số lượng khách du lịch đến 3 tỉnh Hà Nội, Đà Nẵng và TP Hồ Chí Minh trong năm 2020 và năm 2021:

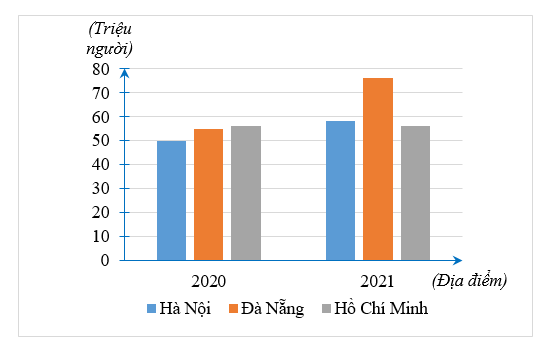
Biểu đồ dưới đây thể hiện số lượng khách du lịch đến 3 tỉnh Hà Nội, Đà Nẵng và TP Hồ Chí Minh trong (ảnh 1)

Hỏi bảng số liệu nào sau đây đúng với biểu đồ trên:

A.

Năm Địa điểm	2020 (triệu người)	2021 (triệu người)
Hà Nội	50	58
Đà Nẵng	55	76
Hồ Chí Minh	56	56

B.

Năm Địa điểm	2020 (triệu người)	2021 (triệu người)
Hà Nội	50	40
Đà Nẵng	55	76
Hồ Chí Minh	56	56

C.

Năm Địa điểm	2020 (triệu người)	2021 (triệu người)
Hà Nội	50	58
Đà Nẵng	76	21
Hồ Chí Minh	56	56

D.

Năm Địa điểm	2020 (triệu người)	2021 (triệu người)
Hà Nội	50	58
Đà Nẵng	55	76
Hồ Chí Minh	60	30

Xem đáp án

Đáp án đúng là: A

Ta thấy trong bảng B, năm 2021 lượng khách đến Hà Nội là 40, nhưng trên biểu đồ, cột biểu diễn lại cao hơn 50. Do đó phương án A là sai.

Ta thấy trong bảng C, năm 2020 lượng khách đến Đà Nẵng là 76, nhưng trên biểu đồ, cột biểu diễn lại thấp hơn 60. Do đó phương án C là sai.

Ta thấy trong bảng D, năm 2020 lượng khách đến Hồ Chí Minh là 76, nhưng trên biểu đồ, cột biểu diễn lại thấp hơn 60. Do đó phương án D là sai.

Vậy ta chọn phương án A.

Câu 7:

Tìm tứ phân vị của mẫu số liệu sau: 11; 20; 1; 30; 4; 25; 15?

A. Q₁ = 4, Q₂ = 15, Q₃ = 25;

B. Q₁ = 4, Q₂ = 11, Q₃ = 25;

C. Q₁ = 4, Q₂ = 15, Q₃ = 20;

D. Q₁ = 4, Q₂ = 11, Q₃ = 20.

Xem đáp án

Đáp án đúng là: A

Sắp xếp lại các phần tử trong mẫu ta được: 1; 4; 11; 15; 20; 25; 30.

Do số phần tử trong mẫu là n = 7 là số lẻ nên số trung vị (tứ phân vị thứ hai) của dãy là số liệu thứ 4, tức là Q2 = 15.

Tứ phân vị thứ nhất là số trung vị của mẫu: 1; 4; 11. Vậy Q1 = 4.

Tứ phân vị thứ ba là số trung vị của mẫu: 20; 25; 30. Vậy Q3 = 25.

Ta chọn phương án A.

Câu 8:

Điểm kiểm tra môn Toán của 24 học sinh được ghi lại trong bảng sau:

7	9	7	5	8	7
5	8	9	4	8	6
7	6	8	9	6	7
6	7	6	8	4	9

Mốt của bảng số liệu trên là:

A. Mo = 5;

B. Mo = 6;

C. Mo = 7;

D. Mo = 8.

Xem đáp án

Đáp án đúng là: C

Ta lập bảng tần số:

Điểm	4	5	6	7	8	9
Số học sinh	2	2	5	6	5	4	n = 24

Ta thấy điểm 7 có tần số lớn nhất nên mốt của mẫu số liệu là Mo = 7.

Câu 9:

Cho mẫu số liệu sau:

Giá trị	15	20	25	30
Tần số tương đối	0,5	0,3	0,1	0,1

Số trung bình là:

A. 18

B. 19

C. 20

D. 25

Xem đáp án

Đáp án đúng là: B

Số trung bình của mẫu là:

$\bar{x}$ = 15 . 0,5 + 20 . 0,3 + 25 . 0,1 + 30 . 0,1 = 19.

Ta chọn phương án B.

Câu 10:

Điểm số của bạn Xuân trong học kì 2 được thống kê như sau:

Số điểm	7	8	9	9,5	10
Số lần	4	5	8	1	1

Khẳng định nào sau đây là đúng?

A.

\bar{x} > M_{e}

;

B.

\bar{x} = M_{e}

;

C.

\bar{x} < M_{e}

;

D. Không so sánh được.

Xem đáp án

Đáp án đúng là: C

Cỡ mẫu của mẫu số liệu là: n = 4 + 5 + 8 + 1 + 1 = 19.

Trung bình của mẫu số liệu là:

$\bar{x} = \frac{7.4 + 8.5 + 9.8 + 9,5.1 + 10.1}{4 + 5 + 8 + 1 + 1} = 8,3947...$

Sắp xếp dãy mẫu số liệu theo thứ tự không giảm, ta được:

7; 7; 7; 7; 8; 8; 8; 8; 8; 9; 9; 9; 9; 9; 9; 9; 9; 9,5; 10.

Cỡ mẫu n = 19 là số lẻ nên số trung vị của mẫu số liệu trên là số liệu thứ 10 của dãy, tức là Me = 9.

Vậy $\bar{x} < M_{e}$ .

Câu 11:

Điểm thi các môn của Lan như sau: 7,0; 9,0; 10; 6,0; 7,3. Khoảng biến thiên của mẫu số liệu trên là:

A. R = 4;

B. R = 9,5;

C. R = 6,5;

D. R = 0.

Xem đáp án

Đáp án đúng là: A

Điểm cao nhất của Lan là: 10.

Điểm thấp nhất của Lan là: 6,0.

Do đó: R = 10 – 6,0 = 4.

Câu 12:

Xác định khoảng tứ phân vị của mẫu số sau: 5; 10; 45; 40; 35; 30; 25; 20; 15.

A.

∆

Q = 10;

B.

∆

Q = 20;

C.

∆

Q = 15;

D.

∆

Q = 25.

Xem đáp án

Đáp án đúng là: D

Sắp xếp mẫu số liệu các điểm ta có: 5; 10; 15; 20; 25; 30; 35; 40; 45.

• Do mẫu có n = 9 là số lẻ nên có tứ phân vị thứ hai là số liệu thứ 5, tức là Q2 = 25.

• Tứ phân vị thứ nhất là trung vị của mẫu 5; 10; 15; 20.

Do mẫu trên có cỡ mẫu là 4 (số chẵn) nên Q1 = $\frac{10 + 15}{2}$ = 12,5.

• Tứ phân vị thứ ba là trung vị của mẫu 30; 35; 40; 45.

Do mẫu trên có cỡ mẫu là 4 (số chẵn) nên Q3 = $\frac{35 + 40}{2}$ = 37,5.

Khi đó khoảng tứ phân vị là ∆Q = Q3 – Q1 = 37,5 – 12,5 = 25.

Câu 13:

Điểm thi học kì các môn của Hoa được thống kê như sau: 10; 8; 6; 6; 9; 8; 5; 8.

Độ lệch chuẩn của mẫu số liệu (làm tròn kết quả đến hàng phần mười) là:

A. S ≈ 1,5;

B. S ≈ 1,7;

C. S ≈ 1,6;

D. S ≈ 2,0.

Xem đáp án

Đáp án đúng là: C

Ta có: số trung bình số điểm của các môn thi học kì của Hoa là:

$\frac{10 + 8 + 6 + 6 + 9 + 8 + 5 + 8}{8} = 7,5.$

Phương sai là:

$S^{2} = \frac{1}{8} (10^{2} + 8^{2} + 6^{2} + 6^{2} + 9^{2} + 8^{2} + 5^{2} + 8^{2}) - {7,5}^{2} = 2,5$

Độ lệch chuẩn là: S = $S = \sqrt{2,5} \approx 1,6.$

Ta chọn phương án C.

Câu 14:

Tìm giá trị ngoại lệ trong mẫu số liệu của cung thủ bắn như sau:

Lần	1	2	3	4	5	6
Điểm	8	8	9	10	0	8

A. 0;

B. 8;

C. 9;

D. 10.

Xem đáp án

Đáp án đúng là: A

Sắp xếp mẫu số liệu như sau: 0; 8; 8; 8; 9; 10.

Ta tìm được tứ phân vị là: Q2 = 8, Q1 = 8, Q3 = 9.

Khoảng tứ phân vị là $∆$ Q = 9 – 8 = 1.

Ta có Q1 – 1,5 $∆$ Q = 8 – 1,5. 1 = 6,5.

Do 0 < Q1 – 1,5 $∆$ Q nên giá trị 0 là giá trị ngoại lệ.

Câu 15:

Trong dịp tết Nguyên đán 2022, xóm Yên Nghĩa có 5 hộ gia đình nấu bánh chưng với số lượng bánh lần lượt là: 20; 10; 15; 5; 22. Phương sai hiệu chỉnh của mẫu số liệu trên là

A. ${\hat{s}}^{2} = 65,73$ ;

B.

{\hat{s}}^{2} = 49,3

;

C.

{\hat{s}}^{2} = 39,44

;

D.

{\hat{s}}^{2} = 32,87

.

Xem đáp án

Đáp án đúng là: B

Mẫu số liệu là: 20; 10; 15; 5; 22.

Số trung bình của mẫu số liệu là:

$\bar{x} = \frac{20 + 10 + 15 + 5 + 22}{5} = 14,4$ .

Khi đó phương sai hiệu chỉnh bằng:

${\hat{s}}^{2} = \frac{1}{5 - 1} [{(20 - 14,4)}^{2} + {(10 - 14,4)}^{2}$

Vậy ta chọn phương án B.

Trắc nghiệm Toán 10 CTST Bài tập cuối chương 6 có đáp án (Phần 2)

Trắc nghiệm Toán 10 CTST Bài tập cuối chương 6 có đáp án (Phần 2) (Thông hiểu)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương