Trắc nghiệm Toán 10 CTST Bài 1. Quy tắc cộng và quy tắc nhân (Phần 2) có đáp án
Trắc nghiệm Toán 10 CTST Bài 1. Quy tắc cộng và quy tắc nhân (Vận dụng) có đáp án
-
210 lượt thi
-
5 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Từ các chữ số 1; 2; 3; 4; 5; 6, có thể lập được bao nhiêu số tự nhiên bé hơn 100?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Các số bé hơn 100 là các số có một chữ số và các số có hai chữ số.
Việc lập các số bé hơn 100 từ các chữ số 1; 2; 3; 4; 5; 6 có hai phương án thực hiện:
Phương án 1: Lập số có một chữ số từ các chữ số 1; 2; 3; 4; 5; 6.
Khi đó có thể lập được 6 số.
Phương án 2: Lập số có hai chữ số từ các chữ số 1; 2; 3; 4; 5; 6.
Gọi là số cần tìm.
Chọn số ở vị trí a, có 6 cách chọn.
Chọn số ở vị trí b, có 6 cách chọn.
Theo quy tắc nhân, ta có 6.6 = 36 cách lập một số có hai chữ số từ các chữ số 1; 2; 3; 4; 5; 6.
Vậy theo quy tắc cộng, ta có tất cả 6 + 36 = 42 số tự nhiên bé hơn 100.
Do đó ta chọn phương án D.
Câu 2:
Một mạng đường giao thông nối các tỉnh A, B, C, D, E, F và G như hình vẽ, trong đó chữ số được viết trên mỗi cạnh là số con đường có thể đi từ tỉnh này đến tỉnh kia, chẳng hạn chữ số 2 viết trên cạnh AB có nghĩa là có 2 con đường nối A và B,...
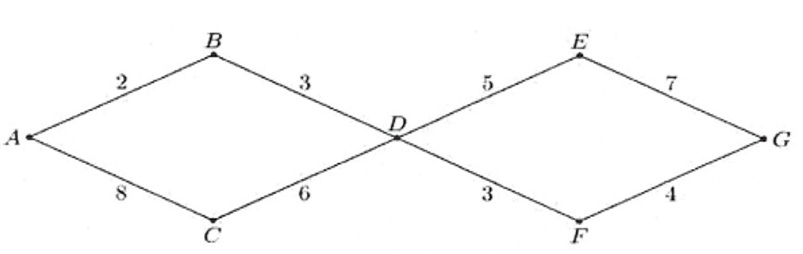
Số con đường từ A đến G là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Ta thấy để đi từ A đến G, ta bắt buộc phải đi qua D.
Bước 1: Đi từ A đến D.
• Phương án 1: Đi từ A, qua B, đến D thì có 2.3 = 6 con đường.
• Phương án 2: Đi từ A, qua C, đến D thì có 8.6 = 48 con đường.
Theo quy tắc cộng, ta có số cách đi từ A đến D là 6 + 48 = 54 con đường.
Bước 2: Đi từ D đến G.
• Phương án 1: Đi từ D, qua E, đến G thì có 5.7 = 35 con đường.
• Phương án 2: Đi từ D, qua F, đến G thì có 3.4 = 12 con đường.
Theo quy tắc cộng, ta có số cách đi từ D đến G là 35 + 12 = 47 con đường.
Vậy theo quy tắc nhân, ta có số cách đi từ A đến G là 54.47 = 2 538 con đường.
Do đó ta chọn phương án B.
Câu 3:
Biển số xe máy của tỉnh A (không gồm kí hiệu địa phương đăng kí xe và seri đăng kí) thì có 5 kí tự, mỗi kí tự là một chữ số thuộc tập hợp {0; 1; 2; 3; 4; 5; 6; 7; 8; 9} và không có biển số xe 000.01. Hỏi nếu hai kí tự đầu tiên đều không nhỏ hơn 7 thì tỉnh A có thể làm được nhiều nhất bao nhiêu biển số xe máy?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Việc chọn một biển số xe gồm 4 công đoạn:
Công đoạn 1: chọn kí tự ở vị trí đầu tiên, có 2 cách chọn một chữ số không nhỏ hơn 7 là 8; 9.
Công đoạn 2: chọn kí tự ở vị trí thứ hai, có 2 cách chọn một chữ số không nhỏ hơn 7 là 8; 9.
Công đoạn 3: chọn kí tự ở vị trí thứ ba, có 10 cách chọn một chữ số thuộc tập hợp {0; 1; 2; 3; 4; 5; 6; 7; 8; 9}.
Công đoạn 4: chọn kí tự ở vị trí thứ tư, có 10 cách chọn một chữ số thuộc tập hợp {0; 1; 2; 3; 4; 5; 6; 7; 8; 9}.
Công đoạn 5: chọn kí tự ở vị trí thứ năm, có 10 cách chọn một chữ số thuộc tập hợp {0; 1; 2; 3; 4; 5; 6; 7; 8; 9}.
Theo quy tắc nhân, ta có tất cả 2.2.10.10.10 = 4 000 cách chọn một biển số xe.
Vậy ta chọn phương án A.
Câu 4:
Số 253 125 000 có bao nhiêu ước số tự nhiên?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Ta có 253 125 000 = 23.34.58.
Do đó mỗi ước số tự nhiên của số 253 125 000 đều có dạng 2m.3n.5p, trong đó 0 ≤ m ≤ 3, 0 ≤ n ≤ 4, 0 ≤ p ≤ 8 và m, n, p ∈ ℕ.
Khi đó:
⦁ m có 4 cách chọn;
⦁ n có 5 cách chọn;
⦁ p có 9 cách chọn.
Theo quy tắc nhân, ta có tất cả 4.5.9 = 180 ước số tự nhiên.
Vậy ta chọn phương án C.
Câu 5:
Cho tập hợp A = {0; 1; 2; 3; 4; 5; 6; 7}. Hỏi từ tập A có thể lập được bao nhiêu số tự nhiên gồm 5 chữ số đôi một khác nhau sao cho một trong 3 chữ số đầu tiên có chữ số 1?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Gọi là số cần tìm.
Trường hợp 1: a = 1.
Khi đó b có 7 cách chọn, c có 6 cách chọn, d có 5 cách chọn và e có 4 cách chọn.
Do đó theo quy tắc nhân, ta có 7.6.5.4 = 840 số được lập.
Trường hợp 2: b = 1 hoặc c = 1 thì có 2 cách.
Khi đó a có 6 cách chọn (vì a ≠ 0 và a ≠ 1).
Ba vị trí còn lại lần lượt có 6, 5, 4 cách chọn.
Do đó theo quy tắc nhân, ta có 2.6.6.5.4 = 1 440 số được lập.
Vậy theo quy tắc cộng, ta có tất cả 840 + 1 440 = 2 280 số được lập.
Do đó ta chọn phương án D.
