Trắc nghiệm Toán 10 Bài 6. Hệ thức lượng trong tam giác có đáp án
Trắc nghiệm Toán 10 Bài 6. Hệ thức lượng trong tam giác có đáp án
-
222 lượt thi
-
15 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Tính diện tích tam giác có ba cạnh lần lượt là 5; 12; 13.
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Nửa chu vi của tam giác là: p=5+12+132=15
Diện tích của tam giác là:
S=√p(p−5)(p−12)(p−13)=√15(15−5)(15−12)(15−13)=30.
Câu 2:
Tam giác ABC có AC=3√3, AB = 3, BC = 6. Tính số đo góc B
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
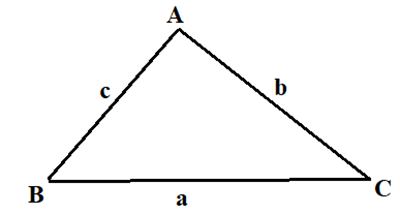
Áp dụng hệ quả của định lý côsin, ta có: cosB=a2+c2−b22ac
⇔cosB=BC2+AB2−AC22AB.BC=62+32−(3√3)22.6.3=12⇒ˆB=60∘.
Câu 3:
Tam giác ABC có các góc ˆA=75∘,ˆB=45∘. Tính tỉ số ABAC.
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
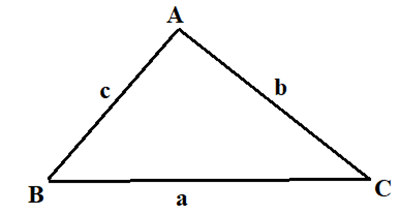
Ta có: bsinB=csinC⇒ABAC=cb=sinCsinB=sin(180∘−75∘−45∘)sin45∘=√62.
Câu 4:
Tam giác ABC có các góc ˆB=30∘,ˆC=45∘, AB = 3. Tính cạnh AC.
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
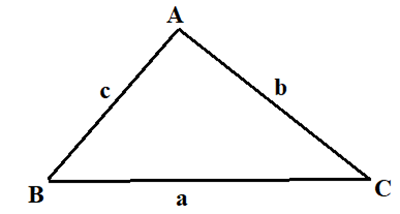
Ta có: bsinB=csinC⇒AC=b=c.sinBsinC=AB.sinBsinC=3.sin300sin450=3√22.
Câu 5:
Tam giác ABC có tổng hai góc B và C bằng 135° và độ dài cạnh BC bằng a. Tính bán kính đường tròn ngoại tiếp tam giác.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có góc A = 180° – 135° = 45°
BCsinA=2R⇒R=BC2sinA=a2sin45∘=a√22.
Câu 6:
Tam giác ABC có A = 120° khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Áp dụng định lí Côsin tại đỉnh A ta có: a2 = b2 + c2 – 2bc.cosA
⇒a2 = b2 + c2 – 2bc.cos120° = b2 + c2 + bc
Câu 7:
Trong tam giác ABC, hệ thức nào sau đây sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Theo định lí hàm số sin ta có: asinA=bsinB=csinC=2R
Suy ra:
+ asinA=bsinB⇒a=b.sinAsinB. Do đó đáp án A đúng.
+ asinA=csinC⇒sinC=c.sinAa. Do đó đáp án B đúng.
+ asinA=2R⇒a=2R.sinA.Do đó đáp án C đúng.
+ bsinB=2R⇒b2=RsinB⇒b2cosB=RtanB. Do đó đáp án D sai.
Câu 8:
Tính diện tích tam giác ABC biết A = 60°; b = 10; c = 20.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Áp dụng công thức : S=12.bc.sinA=12.10.20.sin60∘=50√3.
Câu 9:
Cho tam giác ABC có a = 2, b=√6, c=√3+1. Tính bán kính R của đường tròn ngoại tiếp.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có : cosA=b2+c2−a22bc=√62+(√3+1)2−222.√6.(√3+1)=√22⇒ˆA = 45°.
Do đó : R=a2sinA=22.sin45∘=√2.
Câu 10:
Tam giác ABC vuông tại A có AB = 6 cm; BC = 10 cm. Đường tròn nội tiếp tam giác đó có bán kính r bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có AC=√BC2−AB2=8(cm).
Diện tích tam giác ABC là:S=12AB.AC=24(cm2)
Nửa chu vi p=6+8+102=12 (cm)
Suy ra r=Sp=2412=2(cm).
Câu 11:
Hình bình hành ABCD có AB = a; BC=a√2 và ^BAD=45∘. Khi đó hình bình hành có diện tích bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
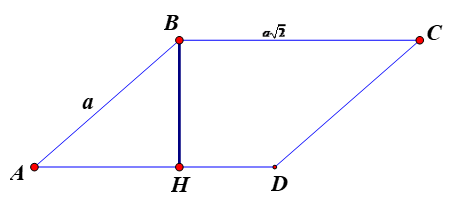
Gọi BH là đường cao của hình bình hành ABCD.
Tam giác BAH vuông tại H, góc ^BAH=^BAD=45∘,
Ta có BH = AB.sin45° = a√22.
Diện tích hình bình hành ABCD là: S=BH.AD=a√22.a√2=a2(đvdt).
Câu 12:
Tính góc C của tam giác ABC biết a ≠ b và a(a2 – c2) = b(b2 – c2).
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: a(a2 – c2) = b(b2 – c2)
⇔ a3 – b3 – c2(a – b) = 0
⇔ (a – b)(a2 + ab + b2) – c2(a – b) = 0
⇔ (a – b)(a2 + ab + b2 – c2) = 0
⇔ a2 + ab + b2 – c2 = 0 (Vì a ≠ b nên a – b ≠ 0)
⇔ a2 + b2 – c2 = – ab
Ta có cosC=a2+b2−c22ab=−ab2ab=−12.
Do đó: ˆC = 120°.
Câu 13:
Tam giác ABC có các cạnh a; b; c thỏa mãn điều kiện:
(a + b + c)(a + b – c) = 3ab. Khi đó số đo của góc C là.
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Trong tam giác ABC ta luôn có: c2 = a2 + b2 – 2ab.cosC.
Hệ thức (a + b + c)(a + b – c) = 3ab
⇔ (a + b)2 – c2 = 3ab
⇔ c2 = a2 + b2 – ab
Suy ra: – 2.cosC = – 1 ⇒cosC=12⇒ˆC=60∘.
Câu 14:
Tam giác ABC có AB = 7; AC = 5 và cos(B+C)=−15. Tính BC
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có: ˆA+ˆB+ˆC=180∘⇔ˆA=180∘−(ˆB+ˆC)
⇒cos(B+C)=cos(180∘−A)=−cosA=−15
⇒cosA=15
Áp dụng định lý côsin trong tam giác, ta có:
BC=√AB2+AC2−2AB.AC.cosA=√72+52−2.7.5.15=2√15.
Câu 15:
Hình bình hành có hai cạnh là 3 và 5, một đường chéo bằng 5. Tìm độ dài đường chéo còn lại.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
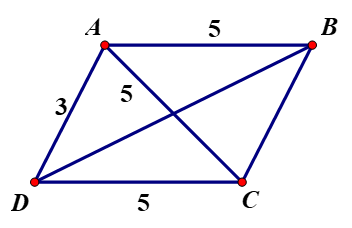
Gọi hình bình hành là ABCD, AD = 3, AB = 5
Gọi α là góc đối diện với đường chéo có độ dài 5
Ta có: cosα=32+52−522.3.5=310
⇒ α là góc nhọn
⇒α=^ADC
⇒ AC = 5
⇒BD2=AD2+AB2−2.AD.AB.cos^BAD=AD2+AB2+2.AD.AB.cos^ADC
(vì ^BAD và ^ADC bù nhau⇒cos^BAD=−cos^ADC)
⇒ BD2 = 32 + 52 + 2.3.5.310 = 43
⇒ BD = √43.
