Giải Toán lớp 6 Bài tập cuối chương 4
Giải Toán 6 trang 22 Tập 2
Toán lớp 6 trang 22 Bài 1: Cuối học kì I, nhà trường khen thưởng mỗi lớp ba học sinh tiêu biểu. Lớp 6A có nhiều bạn vừa học giỏi vừa tích cực tham gia các hoạt động. Cô giáo chủ nhiệm chọn năm bạn xứng đáng nhất để lớp bình chọn. Cô giáo lập phiếu bầu theo mẫu như ở Hình 17. Mỗi học sinh được nhận một phiếu, trên mỗi dòng của phiếu chọn đúng một trong hai ô “Đồng ý” hoặc “Không đồng ý”.
Kết quả bình chọn của cả lớp được cô giáo thống kê lại trong Hình 78.
Hãy lập danh sách ba bạn của lớp 6A được khen thưởng.
|
STT |
Họ và tên |
Đồng ý |
Không đồng ý |
|
1 |
Nguyễn Thị An |
|
|
|
2 |
Vũ Văn Cường |
|
|
|
3 |
Phạm Thu Hoài |
|
|
|
4 |
Bùi Bình Minh |
|
|
|
5 |
Nguyễn Văn Nam |
|
|
Hình 17
|
STT |
Họ và tên |
Đồng ý |
Không đồng ý |
|
1 |
Nguyễn Thị An |
31 |
5 |
|
2 |
Vũ Văn Cường |
20 |
16 |
|
3 |
Phạm Thu Hoài |
33 |
3 |
|
4 |
Bùi Bình Minh |
27 |
9 |
|
5 |
Nguyễn Văn Nam |
18 |
18 |
Hình 18
Lời giải:
Dựa trên kết quả bình chọn, ta thấy:
Ba bạn có kết quả bình chọn đồng ý cao nhất là: Nguyễn Thị An, Phạm Thu Hoài, Bùi Bình Minh
Ta lập được danh sách ba bạn của lớp 6A được khen thưởng như sau:
|
STT |
Họ và tên |
|
1 |
Nguyễn Thị An |
|
3 |
Phạm Thu Hoài |
|
4 |
Bùi Bình Minh |
Toán lớp 6 trang 22 Bài 2: Một câu lạc bộ có 24 thành viên. Người phụ trách thống kê những thành viên có mặt tại câu lạc bộ trong một tuần như ở bảng bên.
a) Hãy nêu đối tượng thống kê và tiêu chí thống kê.
b) Ngày nào có mặt đầy đủ tất cả các thành viên của câu lạc bộ?
c) Tính tổng số lượt người vắng mặt tại câu lạc bộ trong tuần
|
Thứ |
Số thành viên có mặt |
|
Thứ Hai |
|
|
Thứ Ba |
|
|
Thứ Tư |
|
|
Thứ Năm |
|
|
Thứ Sáu |
|
|
|
|
Lời giải:
a) Đối tượng thống kê: Các thứ trong một tuần (không tính thứ 7 và chủ nhật).
Tiêu chí thống kê là số thành viên có mặt tương ứng với từng thứ.
b) Quan sát biểu đồ, ta có:
Thứ hai, có 18 thành viên có mặt.
Thứ ba, có 20 thành viên có mặt.
Thứ tư, có 24 thành viên có mặt.
Thứ năm, có 23 thành viên có mặt.
Thứ sáu, có 21 thành viên có mặt.
Ngày có mặt đầy đủ tất cả các thành viên của câu lạc bộ là thứ tư.
c) Quan sát biểu đồ, ta có:
Thứ hai, có 24 – 18 = 6 thành viên vắng mặt.
Thứ ba, có 24 – 20 = 4 thành viên vắng mặt.
Thứ tư, có 24 – 24 = 0 thành viên vắng mặt.
Thứ năm, có 24 – 23 = 1 thành viên vắng mặt.
Thứ sáu, có 24 – 21 = 3 thành viên vắng mặt.
Tổng số lượng người vắng mặt tại câu lạc bộ trong tuần là:
6 + 4 + 0 + 1 + 3 = 14 (người).
Vậy tổng số lượng người vắng mặt tại câu lạc bộ trong tuần là 14 người.
Giải Toán 6 trang 23 Tập 2
Toán lớp 6 trang 23 Bài 3: Do tác động của En Ni-nô (El Nino), mùa mưa năm 2015 đến muộn và kết thúc sớm nên mực nước sông Mê Kông xuống thấp nhất trong 90 năm qua. Xâm nhập mặn đã ảnh hưởng đến hàng trăm nghìn héc-ta lúa.
Biểu đồ ở Hình 19 cho biết diện tích lúa bị hại do xâm nhập mặn vào cuối năm 2015 và đầu năm 2016 của một số tỉnh. Tính tổng diện tích lúa bị hại của các tỉnh đó.
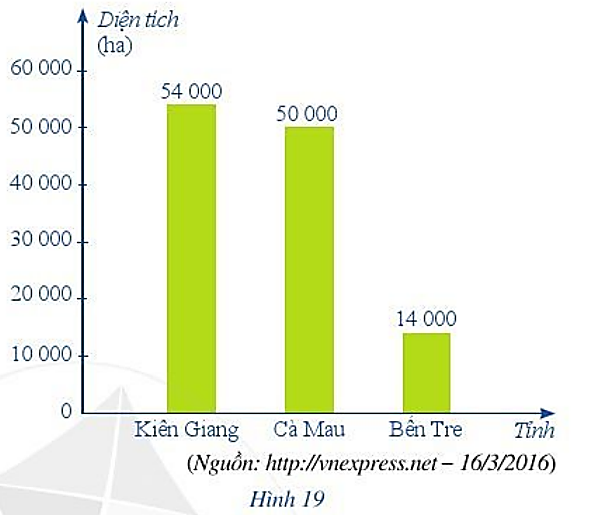
Lời giải:
Tổng diện tích lúa bị hại do xâm nhập mặn vào cuối năm 2015 và đầu năm 2016 của các tỉnh là: 54 000 + 50 000 + 14 000 = 118 000 (ha).
Vậy tổng diện tích lúa bị hại do xâm nhập mặt vào cuối năm 2015 và đầu năm 2016 là 118 000 (ha).
Toán lớp 6 trang 23 Bài 4: Biểu đồ cột kép ở Hình 20 biểu diễn sản lượng cà phê và gạo xuất khẩu của Việt Nam trong ba năm 2017, 2018, 2019.
a) Tính tổng lượng cà phê xuất khẩu trong ba năm 2017, 2018, 2019.
b) Sản lượng cà phê xuất khẩu năm 2018 nhiều hơn sản lượng cà phê xuất khẩu năm 2019 là bao nhiêu?
c) Tính tổng lượng gạo xuất khẩu trong ba năm 2017, 2018, 2019.
d) Sản lượng gạo xuất khẩu năm 2019 nhiều hơn sản lượng gạo xuất khẩu năm 2018 là bao nhiêu?
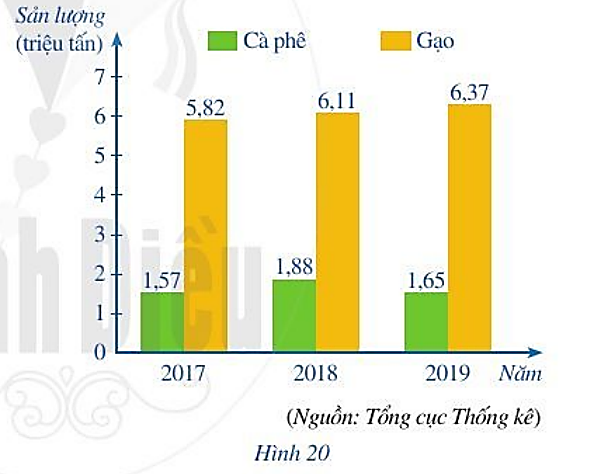
Lời giải:
a) Tổng lượng cà phê xuất khẩu trong ba năm 2017, 2018, 2019 là:
1,57 + 1,88 + 1,65 = 5,1 (triệu tấn).
Vậy tổng lượng cà phê xuất khẩu trong ba năm 2017, 2018, 2019 là 5,1 triệu tấn.
b) Sản lượng cà phê xuất khẩu năm 2018 nhiều hơn sản lượng cà phê xuất khẩu năm 2019 là: 1,88 – 1,65 = 0,23 (triệu tấn).
Vậy sản lượng cà phê xuất khẩu năm 2018 nhiều hơn sản lượng cà phê xuất khẩu năm 2019 là 0,23 triệu tấn.
c) Tổng lượng gạo xuất khẩu trong ba năm 2017, 2018, 2019 là:
5,82 + 6,11 + 6,37 = 18,3 (triệu tấn).
Vậy tổng lượng gạo xuất khẩu trong ba năm 2017, 2018, 2019 là 18,3 triệu tấn.
d) Sản lượng gạo xuất khẩu năm 2019 nhiều hơn sản lượng cà phê xuất khẩu năm 2018 là: 6,37 – 6,11 = 0,26 (triệu tấn).
Vậy sản lượng gạo xuất khẩu năm 2019 nhiều hơn sản lượng cà phê xuất khẩu năm 2018 là 0,26 triệu tấn.
Toán lớp 6 trang 23 Bài 5: Biểu đồ cột kép ở Hình 21 biểu diễn số tiền Việt Nam thu được khi xuất khẩu cà phê và xuất khẩu gạo trong ba năm 2017, 2018, 2019.
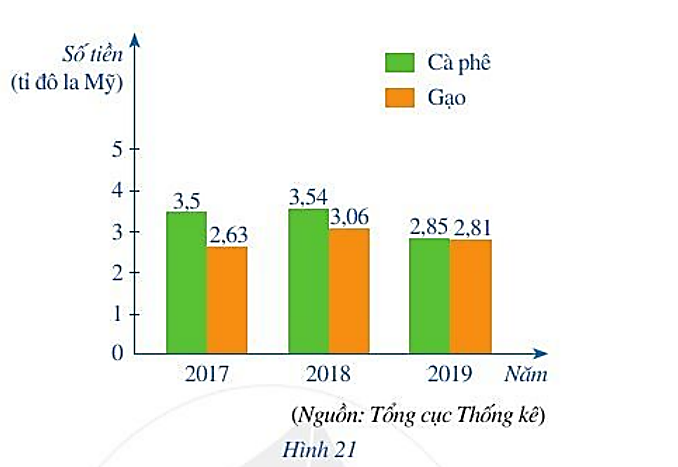
a) Tính tổng số tiền thu được khi xuất khẩu cà phê trong ba năm 2017, 2018, 2019.
b) Số tiền thu được khi xuất khẩu cà phê năm 2018 nhiều hơn số tiền thu được khi xuất khẩu
. cà phê năm 2019 là bao nhiêu?
c) Tính tổng số tiền thu được khi xuất khẩu gạo trong ba năm 2017, 2018, 2019.
d) Số tiền thu được khi xuất khẩu gạo năm 2018 nhiều hơn số tiền thu được khi xuất khẩu gạo năm 2019 là bao nhiêu?
e) Trong ba năm 2017, 2018, 2019, năm nào số tiền thu được khi xuất khẩu gạo là nhiều nhất? Ít nhất?
Lời giải:
a) Tổng số tiền thu được khi xuất khẩu cà phê trong ba năm 2017, 2018, 2019 là:
3,5 + 3,54 + 2,85 = 9,89 (tỉ đô la Mỹ)
Vậy tổng số tiền thu được khi xuất khẩu cà phê trong ba năm 2017, 2018, 2019 là 9,89 tỉ đô la Mỹ.
b) Số tiền thu được khi xuất khẩu cà phê năm 2018 nhiều hơn số tiền thu được khi xuất khẩu cà phê năm 2019 là:
3,54 – 2,85 = 0,69 (tỉ đô la Mỹ)
Vậy số tiền thu được khi xuất khẩu cà phê năm 2018 nhiều hơn số tiền thu được khi xuất khẩu cà phê năm 2019 là 0,69 tỉ đô la Mỹ.
c) Tổng số tiền thu được khi xuất khẩu gạo trong ba năm 2017, 2018, 2019 là:
2,63 + 3,06 + 2,81 = 8,5 (tỉ đô la Mỹ)
Vậy tổng số tiền thu được khi xuất khẩu gạo trong ba năm 2017, 2018, 2019 là 8,5 tỉ đô la Mỹ.
d) Số tiền thu được khi xuất khẩu gạo năm 2018 nhiều hơn số tiền thu được khi xuất khẩu gạo năm 2019 là:
3,06 – 2,81 = 0,25 (tỉ đô la Mỹ).
Vậy số tiền thu được khi xuất khẩu gạo năm 2018 nhiều hơn số tiền thu được khi xuất khẩu gạo năm 2019 là 0,25 tỉ đô la Mỹ.
e) Vì 3,06 > 2,81 > 2,63 nên ta có:
Số tiền thu được khi xuất khẩu gạo là nhiều nhất vào năm 2018 với 3,06 tỉ đô la Mỹ.
Số tiền thu được khi xuất khẩu gạo là ít nhất vào năm 2017 với 2,63 tỉ đô la Mỹ.
Giải Toán 6 trang 24 Tập 2
Toán lớp 6 trang 24 Bài 6: Tung một đồng xu 15 lần liên tiếp. Hãy ghi kết quả thống kê theo mẫu sau:
|
Lần tung |
Kết quả tung |
Số lần xuất hiện mặt N |
Số lần xuất hiện mặt S |
|
1 |
? |
? |
? |
|
… |
? |
Tính xác suất thực nghiệm:
a) Xuất hiện mặt N;
b) Xuất hiện mặt S.
Lời giải:
Tung một đồng xu 15 lần liên tiếp, ta được bảng kết quả sau:
|
Lần tung |
Kết quả tung |
Số lần xuất hiện mặt N |
Số lần xuất hiện mặt S |
|
1 |
N |
7 |
8 |
|
2 |
N |
||
|
3 |
S |
||
|
4 |
S |
||
|
5 |
S |
||
|
6 |
S |
||
|
7 |
N |
||
|
8 |
S |
||
|
9 |
N |
||
|
10 |
N |
||
|
11 |
N |
||
|
12 |
S |
||
|
13 |
S |
||
|
14 |
N |
||
|
15 |
S |
a) Xác suất thực nghiệm xuất hiện mặt N là:
b) Xác suất thực nghiệm xuất hiện mặt S là:
Toán lớp 6 trang 24 Bài 7: Gieo một xúc xắc 10 lần liên tiếp. Hãy ghi kết quả thống kê theo mẫu sau:
|
Lần gieo |
Kết quả gieo |
Tổng số lần xuất hiện |
|||||
|
Mặt 1 chấm |
Mặt 2 chấm |
Mặt 3 chấm |
Mặt 4 chấm |
Mặt 5 chấm |
Mặt 6 chấm |
||
|
1 |
? |
? |
? |
? |
? |
? |
? |
|
… |
? |
||||||
Tính xác suất thực nghiệm:
a) Xuất hiện mặt 1 chấm;
b) Xuất hiện mặt 2 chấm;
c) Xuất hiện mặt 3 chấm;
d) Xuất hiện mặt 4 chấm;
e) Xuất hiện mặt 5 chấm;
g) Xuất hiện mặt 6 chấm.
Lời giải:
Gieo một xúc xắc 10 lần liên tiếp, ta có kết quả ở bảng sau:
|
Lần gieo |
Kết quả gieo |
Tổng số lần xuất hiện |
|||||
|
Mặt 1 chấm |
Mặt 2 chấm |
Mặt 3 chấm |
Mặt 4 chấm |
Mặt 5 chấm |
Mặt 6 chấm |
||
|
1 |
6 |
0 |
2 |
3 |
1 |
2 |
2 |
|
2 |
5 |
||||||
|
3 |
3 |
||||||
|
4 |
5 |
||||||
|
5 |
6 |
||||||
|
6 |
2 |
||||||
|
7 |
4 |
||||||
|
8 |
3 |
||||||
|
9 |
2 |
||||||
|
10 |
3 |
||||||
a) Xác suất thực nghiệm xuất hiện mặt một chấm là:
b) Xác suất thực nghiệm xuất hiện mặt hai chấm là:
c) Xác suất thực nghiệm xuất hiện mặt ba chấm là:
d) Xác suất thực nghiệm xuất hiện mặt bốn chấm là:
e) Xác suất thực nghiệm xuất hiện mặt năm chấm là:
d) Xác suất thực nghiệm xuất hiện mặt sáu chấm là:
Xem thêm lời giải SGK Toán lớp 6 sách Cánh diều hay, chi tiết khác:
Bài 3: Mô hình xác suất trong một số trò chơi và thí nghiệm đơn giản
Bài 4: Xác xuất thực nghiệm trong một số trò chơi và thí nghiệm đơn giản
Bài 1: Phân số với tử và mẫu là số nguyên




