Giải Tin học 10 Bài 2: Thực hành về các phép toán bit và hệ nhị phân
Bài 1. Chuyển đổi biểu diễn số ở hệ thập phân sang hệ nhị phân
Trả lời:
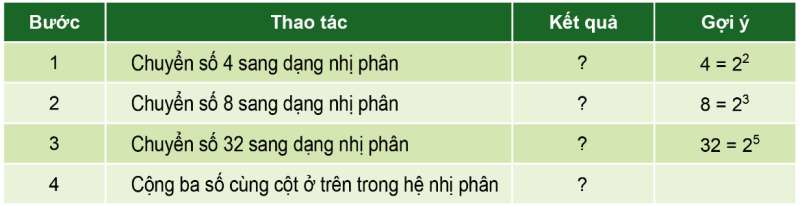
| Bước | Thao tác | Kết quả |
| 1 | Chuyển số 4 sang dạng nhị phân | 100 |
| 2 | Chuyển số 8 sang dạng nhị phân | 1000 |
| 3 | Chuyển số 32 sang dạng nhị phân | 100000 |
| 4 | Cộng ba số cùng cột ở trên trong hệ nhị phân | 101100 |
Bài 2. Cộng và nhân hai số nhị phân
Trả lời:
Bảng 1:
|
213 |
11010101 |
|
77 |
1001101 |
|
290 |
100100010 |
|
16401 |
100000000010001 |
Bảng 2:
|
101 |
1100101 |
|
22 |
10110 |
|
123 |
1111011 |
|
2222 |
100010101110 |
Bảng 3:
|
50 |
110010 |
|
20 |
10100 |
|
70 |
1000110 |
|
1000 |
1111101000 |
Bài 3. Tính số bù của một số nhị phân
2) Cho số nhị phân x. Kết quả của phép toán ![]() gọi là số bù 2 của x. Em hãy viết số bù 2 của số 44 ở hệ nhị phân.
gọi là số bù 2 của x. Em hãy viết số bù 2 của số 44 ở hệ nhị phân.
Trả lời:
a) Số bù 1 có thể có được do đảo tất cả các bit có trong số nhị phân.
Số 44 ở hệ nhị phân là: 101100
Vậy số bù 1 của số 44 ở hệ nhị phân là: 010011.
b) Số bù 2 của số 44 ở hệ nhị phân: 010011 + 1= 010100.
Bài 4. Khám phá ý nghĩa của số bù của một số nhị phân
Trả lời:
- Số nhị phân x có giá trị thập phân là 44: 00101100.
- Số bù 1 của số trên là: 11010011.
- Số bù 2 của số trên là: 11010011+ 1 = 11010100.
Tổng số nhị phân x và số bù 2 của nó là: 00101100 + 11010100 = 100000000.
Vận dụng (trang 138)
- Em hãy dùng phép toán bit để tạo ra KetQua là dãy 10 bit, biểu diễn kết quả chấm từng câu hỏi, dúng là 1, sai là 0.
- Em hãy tính điểm cho thí sinh theo thang điểm 10.
Trả lời:
Ta sẽ gọi dãy bit DapAn là 0000000000 (10 số 0).
Dãy bit TraLoi của thí sinh sẽ gồm 10 bit toàn 0 và 1.
Phép cộng dãy bit TraLoi với DapAn sẽ cho ta dãy bit KetQua bởi vì: Nếu thí sinh trả lời đúng thì 1 + 0 = 1 (kết quả đúng), nếu thí sinh trả lời sai thì 0 + 0 = 0 (kết quả sai).
Điểm của thí sinh sẽ tính bằng số lượng bit có giá trị bằng 1 của KetQua.
Xem thêm các bài giải SGK Tin học lớp 10 Cánh diều hay, chi tiết khác:
Bài 2: Dự án nhỏ: Tìm hiểu về lập trình web, lập trình trò chơi và lập trình cho thiết bị di động
Bài 1: Hệ nhị phân và ứng dụng




