Xét tất cả các số thực x, y sao cho $a^{4x-{\log }_5{x}^2}\le {25}^{40-y^2}$  đúng với mọi số thực dương a. Giá trị lớn nhất của biểu thức P = x² + y² + x – 3y bằng:

Ta có:

$a^{4x-{\log }_5{x}^2}\le {25}^{40-y^2}$

⇔ ${\log }_5{a}^{4x-{\log }_5{a}^2}\le {\log }_5{25}^{40-y^2}$

⇔ $\left(4x-2{\log }_{5}a\right){\log }_5\le 2\left(40-y^2\right)$

⇔ ${\log }_5^{2}a-2x{\log }_{5}a+40-y^2\ge 0$ (*) 

Coi (*) là phương trình bậc hai ẩn log₅a

Để (*) đúng với mọi số thực dương a thì:

∆' ≤ 0 ⇔ x² – (40 – y²) ≤ 0 ⇔ x² + y² – 40 ≤ 0 (1)

Ta có biểu thức (1) là hình tròn (C₁) tâm O(0;0), bán kình R₁ = $2\sqrt{10}$

Mặt khác P = x² + y² + x – 3y ⇔ x² + y² + x – 3y – P = 0 là phương trình đường trogn (C₂) tâm I$\left(\frac{-1}{2};\frac{3}{2}\right)$ , bán kính R₂ = $\frac{1}{2}\sqrt{10+4P}$

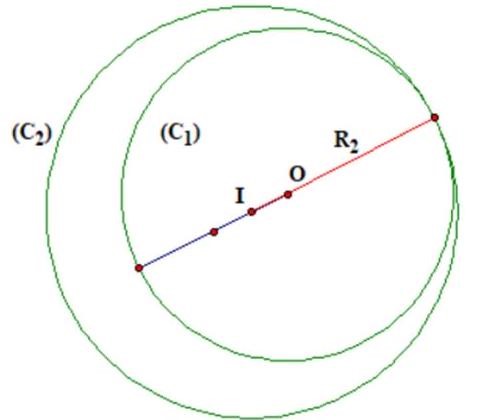
Để tồn tại điểm chung của đường tròn (C₁) và (C₂) thì:

R₂ ≤ R₁ + OI ⇔ $\frac{1}{2}\sqrt{10+4P}$ ≤ $2\sqrt{10}$  + $\frac{1}{2}\sqrt{10}$

⇔ $\sqrt{10+4P}\le 5\sqrt{10}$ ⇔ P ≤ 60.

Vậy P_max = 60.