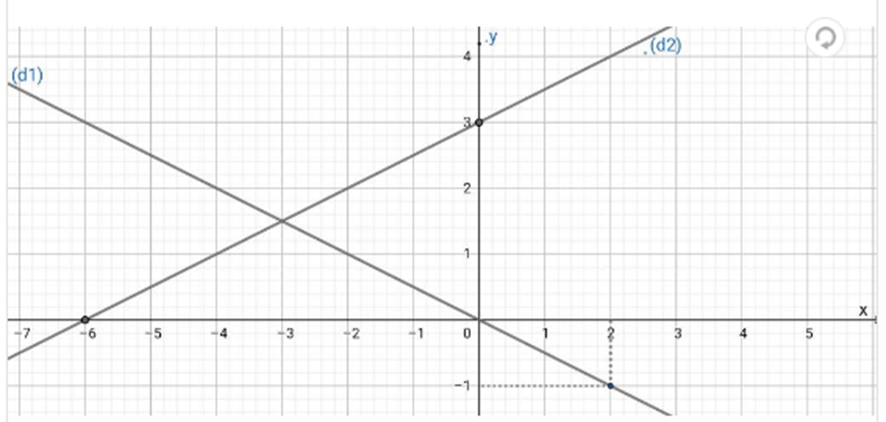
Vẽ trên cùng một mặt phẳng tọa độ Oxy đồ thị của các hàm số sau: y = 1/2 x (d1) và y = 1/2
+) Vẽ đồ thị hàm số \[\left( {{{\rm{d}}_{\rm{1}}}} \right){\rm{: y = - }}\frac{{\rm{1}}}{{\rm{2}}}{\rm{x}}\]
Với x = 0→ y = 0 ta có điểm (0; 0)
Với \[{\rm{x = 2}} \to {\rm{y = - }}\frac{{\rm{1}}}{{\rm{2}}}{\rm{ }}{\rm{. 2 = - 1}}\] ta có điểm (2; −1)
Vẽ đường thẳng đi qua hai điểm (0; 0); (2; −1) ta được (d1)
+) Vẽ đồ thị hàm số(d2):y=12x+3
Với x = 0 → y = 3 ta có điểm (0; 3)
Với \[{\rm{y = 0}} \Rightarrow \frac{{\rm{1}}}{{\rm{2}}}{\rm{x + 3 = 0}} \Rightarrow {\rm{x = - 6}}\] ta có điểm (−6; 0)
Vẽ đường thẳng đi qua hai điểm (0; 3); (−6; 0) ta được (d2)
+) Phương trình hoành độ giao điểm của (d3):y=2x+bvà (d2):y=12x+3là
2x+b=12x+3
⇔2x−12x=3−b
⇔32x=3−b
⇔3x=6−2b
⇒x=2−23b
Thay x=2−23bvào (d2):y=12x+3
⇒y=12.(2−23b)+3=1−13b+3=4−13b
Vì giao điểm của (d2); (d3) có tung độ và hoành độ đối nhau
→ x + y = 0
⇒2−23b+4−13b=0
\[ \Leftrightarrow {\rm{ - }}\frac{{\rm{2}}}{{\rm{3}}}{\rm{b - }}\frac{{\rm{1}}}{{\rm{3}}}{\rm{b = - 4 - 2}}\]
\[ \Leftrightarrow - {\rm{b = - 6}}\]
⇔b=6
Vậy b=6thỏa mãn đề bài