Vẽ trên cùng một mặt phẳng tọa độ Oxy đồ thị của các hàm số sau:

y =$\frac{{ - 1}}{2}x$ (d₁) và y = $\frac{1}{2}x$ + 3 (d₂).

Xác định b để đường thẳng (d₃) y = 2x + b cắt (d₂) tại điểm có tung độ và hoành độ đối nhau.

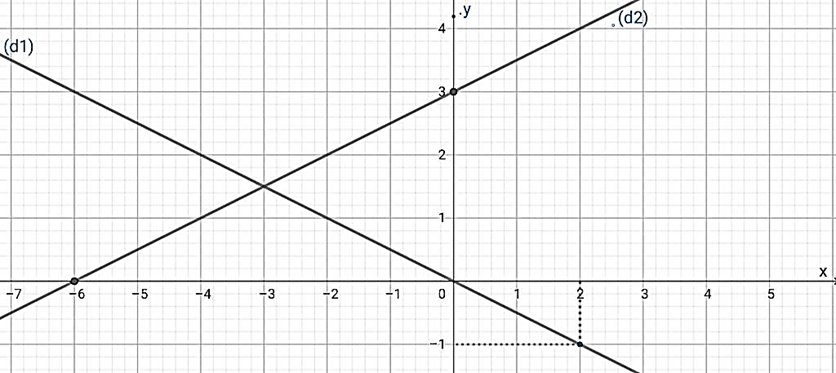
+) Vẽ đồ thị hàm số (d₁): y = $\frac{{ - 1}}{2}x$

Với x = 0 ⇒ y = 0 ta có điểm (0;0)(

Với x = 2 ⇒ y = $\frac{{ - 1}}{2}$.2 = −1 ta có điểm (2;−1)

Vẽ đường thẳng đi qua hai điểm (0;0);(2;−1) ta được (d₁)

+) Vẽ đồ thị hàm số (d₂):y =$\frac{1}{2}x$+ 3

Với x = 0 ⇒ y = 3 ta có điểm (0;3)

Với y = 0 ⇒$\frac{1}{2}x$+ 3 = 0 ⇒ x = −6 ta có điểm (−6;0)

Vẽ đường thẳng đi qua hai điểm (0;3);(−6;0) ta được (d₂)

Phương trình hoành độ giao điểm của (d₃): y = 2x + b và (d₂): y =$\frac{1}{2}x$+ 3

2x + b = $\frac{1}{2}x$+ 3

⇔ $\frac{3}{2}x = 3 - b$

⇔ x = $2 - \frac{2}{3}b$

Thay x = $2 - \frac{2}{3}b$ vào (d₂) ta được: y = $\frac{1}{2}\left( {2 - \frac{2}{3}b} \right) + 3 = 4 - \frac{1}{3}b$

Vì giao điểm của (d₂); (d₃) có tung độ và hoành độ đối nhau

⇒ x + y = 0

⇔ $2 - \frac{2}{3}b + 4 - \frac{1}{3}b = 0$

⇔ –b = – 6

⇔ b = 6

Vậy b = 6.