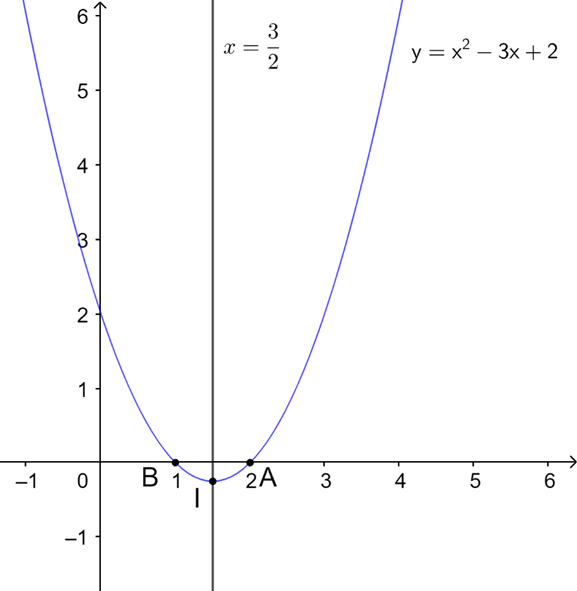
Vẽ đồ thị hàm số y = x² − 3x + 2

+) Ta có đỉnh của đồ thị hàm số là \(I\left( {\frac{3}{2};\; - \frac{1}{4}} \right)\)

+) Với x = 0 Þ y = 2

+) Hoành độ giao điểm của đồ thị hàm số trên và trục Ox là nghiệm của phương trình:

x² − 3x + 2 = 0

Û (x − 1)(x − 2) = 0

Vậy x = 1 và x = 2

Suy ra y = x² − 3x + 2 cắt trục hoành tại hai điểm A(2; 0) và B(1; 0)

y = x² − 3x + 2 nhận \(x = \frac{3}{2}\) là trục đối xứng