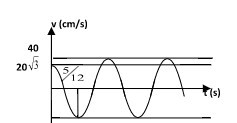
Vận tốc của một vật dao động điều hòa biến thiên theo đồ thị như hình vẽ. Lấy pi ^2 = 10, phương trình dao động của vật là A. x = 2 căn bậc hai của 10cos ( 2pi t + pi /3)( cm). B. x = 2
27
21/07/2024
Vận tốc của một vật dao động điều hòa biến thiên theo đồ thị như hình vẽ. Lấy \({\pi ^2}\) = 10, phương trình dao động của vật là
A. \(x = 2\sqrt {10} \cos \left( {2\pi t + \frac{\pi }{3}} \right)\left( {cm} \right)\).
B. \(x = 2\sqrt {10} \cos \left( {\pi t + \frac{\pi }{3}} \right)\left( {cm} \right)\).
C. \(x = 2\sqrt {10} \cos \left( {2\pi t - \frac{\pi }{3}} \right)\left( {cm} \right)\).
D. \(x = 2\sqrt {10} \cos \left( {\pi t - \frac{\pi }{3}} \right)\left( {cm} \right)\).
Trả lời
Lời giải
Lúc t = 0: \(v = 20\sqrt 3 \Rightarrow \sin \varphi = - \frac{{\sqrt 3 }}{2}\)và do vận tốc đang giảm nên vật ở li độ dương và đang đi về biên dương.
\( \Rightarrow \varphi = - \frac{\pi }{3} \Rightarrow x = A\cos \left( { - \frac{\pi }{3}} \right) = \frac{A}{2}\)
Thời gian tương ứng từ x = A/2 đến vị trí cân bằng theo chiều âm lần thứ nhất:
\(t = \frac{T}{6} + \frac{T}{4} = \frac{5}{{12}}T = \frac{5}{{12}}(s) \Rightarrow T = 1 \Rightarrow \omega = 2\pi \left( {rad/s} \right) \Rightarrow A = \frac{{{v_{\max }}}}{\omega } = \frac{{40}}{{2\pi }} = 2\sqrt {10} \left( {cm} \right)\)
Vậy \(x = 2\sqrt {10} \cos \left( {2\pi t - \frac{\pi }{3}} \right)\left( {cm} \right)\)
Đáp án đúng: C
