Vận dụng phép đối xứng tâm và đối xứng trục để cắt hoa văn trang trí theo hướng dẫn sau: – Lấy một tờ giấy

Bài 7 trang 25 Chuyên đề Toán 11: Vận dụng phép đối xứng tâm và đối xứng trục để cắt hoa văn trang trí theo hướng dẫn sau:

– Lấy một tờ giấy hình vuông, gấp đôi, gấp tư rồi gấp làm tám (Hình 14a).

– Vẽ hoa và lá trên bề mặt tam giác (Hình 14b).

– Dùng kéo cắt theo đường đã vẽ (Hình 14c).

– Trải phẳng tờ giấy ra để thấy hoa văn trang trí gồm hoa và lá (Hình 14d).

Tìm tâm đối xứng và trục đối xứng của hoa văn vừa làm.

Trả lời

⦁ Giả sử ta chọn điểm O là giao điểm của các đường nếp gấp trên hình hoa văn vừa làm (như hình vẽ).

Lấy điểm A bất kì trên hình hoa văn vừa làm sao cho A ≠ O.

Khi đó ta luôn xác định được một điểm A’ trên hình hoa văn vừa làm sao cho A’ = Đ_O(A).

Lấy điểm B trùng O. Khi đó ta có B = Đ_O(B).

Tương tự như vậy, ta chọn các điểm khác bất kì nằm trên hình hoa văn vừa làm, ta đều xác định được ảnh của các điểm đó qua Đ_O trên hình hoa văn vừa làm.

Do đó phép đối xứng tâm O biến hình hoa văn vừa làm thành chính nó.

Vậy O là tâm đối xứng của hình hoa văn vừa làm.

⦁ Giả sử ta chọn đường thẳng d trên hình hoa văn vừa làm như hình vẽ.

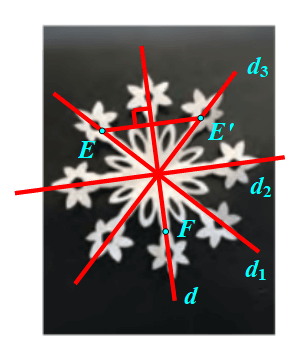
Lấy điểm E trên hình hoa văn vừa làm nhưng không nằm trên đường thẳng d.

Ta đặt E’ = Đ_d(E).

Khi đó E’ nằm trên hình hoa văn vừa làm.

Lấy điểm F trên hình hoa văn vừa làm và nằm trên đường thẳng d.

Ta thấy F = Đ_d(F).

Tương tự như vậy, ta chọn các điểm khác bất kì trên hình hoa văn vừa làm, ta đều xác định được ảnh của điểm đó qua Đ_d trên hình hoa văn vừa làm.

Do đó phép đối xứng trục d biến hình hoa văn vừa làm thành chính nó.

Vậy d là trục đối xứng của hình hoa văn vừa làm.

Chú ý: Hình hoa văn vừa làm có 4 trục đối xứng (d, d₁, d₂, d₃).

Xem thêm các bài giải Chuyên đề Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Phép tịnh tiến

Bài 3: Phép đối xứng trục

Bài 4: Phép đối xứng tâm

Bài 5: Phép quay

Bài 6: Phép vị tự

Bài 7: Phép đồng dạng