Câu hỏi:
09/04/2024 77
Từ một tấm bìa carton hình vuông có độ dài cạnh bằng 60 cm, người ta cắt bốn hình vuông bằng nhau ở bốn góc rồi gập thành một chiếc hộp có dạng hình hộp chữ nhật không có nắp (H.1.14). Tính cạnh của các hình vuông bị cắt sao cho thể tích của chiếc hộp là lớn nhất.
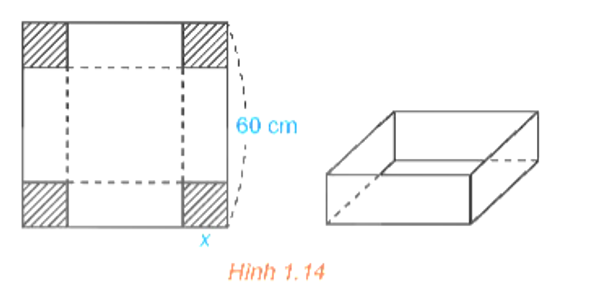
Từ một tấm bìa carton hình vuông có độ dài cạnh bằng 60 cm, người ta cắt bốn hình vuông bằng nhau ở bốn góc rồi gập thành một chiếc hộp có dạng hình hộp chữ nhật không có nắp (H.1.14). Tính cạnh của các hình vuông bị cắt sao cho thể tích của chiếc hộp là lớn nhất.

Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Gọi x (cm) là độ dài cạnh của các hình vuông nhỏ được cắt ở bốn góc của tấm bìa.
Điều kiện 0 < x < 30.
Khi cắt bỏ bốn hình vuông nhỏ có cạnh x (cm) ở bốn góc và gập lên thì ta được một chiếc hộp chữ nhật không có nắp, có đáy là hình vuông với độ dài cạnh bằng (60 – 2x) (cm) và chiều cao bằng x (cm).
Thể tích của chiếc hộp này là: V(x) = (60 – 2x)2.x = 4x3 – 240x2 + 3600x (cm3).
Ta có V'(x) = 12x2 – 480x + 3600;
V'(x) = 0 Û 12x2 – 480x + 3600 = 0 Û x = 10 (thỏa mãn) hoặc x = 30 (loại).
Lập bảng biến thiên
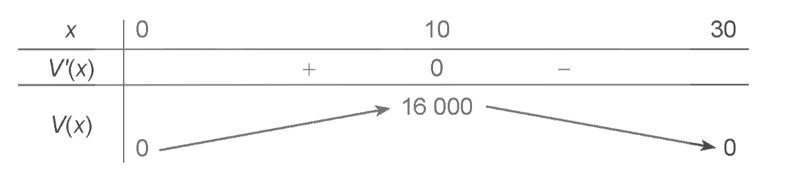
Vậy để thể tích của chiếc hộp lớn nhất thì độ dài cạnh của các hình vuông nhỏ phải cắt là 10 cm.
Gọi x (cm) là độ dài cạnh của các hình vuông nhỏ được cắt ở bốn góc của tấm bìa.
Điều kiện 0 < x < 30.
Khi cắt bỏ bốn hình vuông nhỏ có cạnh x (cm) ở bốn góc và gập lên thì ta được một chiếc hộp chữ nhật không có nắp, có đáy là hình vuông với độ dài cạnh bằng (60 – 2x) (cm) và chiều cao bằng x (cm).
Thể tích của chiếc hộp này là: V(x) = (60 – 2x)2.x = 4x3 – 240x2 + 3600x (cm3).
Ta có V'(x) = 12x2 – 480x + 3600;
V'(x) = 0 Û 12x2 – 480x + 3600 = 0 Û x = 10 (thỏa mãn) hoặc x = 30 (loại).
Lập bảng biến thiên

Vậy để thể tích của chiếc hộp lớn nhất thì độ dài cạnh của các hình vuông nhỏ phải cắt là 10 cm.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Một nhà sản xuất muốn thiết kế một chiếc hộp có dạng hình hộp chữ nhật không có nắp, có đáy là hình vuông và diện tích bề mặt bằng 108 cm2 như Hình 1.17. Tìm các kích thước của chiếc hộp sao cho thể tích của hộp là lớn nhất.
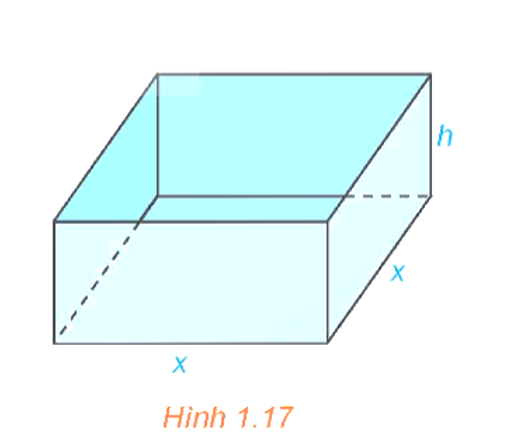
Một nhà sản xuất muốn thiết kế một chiếc hộp có dạng hình hộp chữ nhật không có nắp, có đáy là hình vuông và diện tích bề mặt bằng 108 cm2 như Hình 1.17. Tìm các kích thước của chiếc hộp sao cho thể tích của hộp là lớn nhất.

Câu 2:
Trong các hình chữ nhật có chu vi là 24 cm, hãy tìm hình chữ nhật có diện tích lớn nhất?
Trong các hình chữ nhật có chu vi là 24 cm, hãy tìm hình chữ nhật có diện tích lớn nhất?
Câu 3:
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:
b) trên khoảng (1; +∞).
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:
b) trên khoảng (1; +∞).
Câu 4:
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
a) y = 2x3 – 3x2 + 5x + 2 trên đoạn [0; 2];
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
a) y = 2x3 – 3x2 + 5x + 2 trên đoạn [0; 2];
Câu 5:
Một nhà sản xuất cần làm ra những chiếc bình có dạng hình trụ với dung tích 1000 cm3. Mặt trên và mặt dưới của bình được làm bằng vật liệu có giá 1,2 nghìn đồng/cm2, trong khi mặt bên của bình được làm bằng vật liệu có giá 0,75 nghìn đồng/cm2. Tính các kích thước của bình để chi phí vật liệu sản xuất mỗi chiếc bình là nhỏ nhất.
Một nhà sản xuất cần làm ra những chiếc bình có dạng hình trụ với dung tích 1000 cm3. Mặt trên và mặt dưới của bình được làm bằng vật liệu có giá 1,2 nghìn đồng/cm2, trong khi mặt bên của bình được làm bằng vật liệu có giá 0,75 nghìn đồng/cm2. Tính các kích thước của bình để chi phí vật liệu sản xuất mỗi chiếc bình là nhỏ nhất.
Câu 6:
Cho hàm số y = f(x) = x2 – 2x với x ∈ [0; 3], có đồ thị như hình 1.15.
![Cho hàm số y = f(x) = x^2 – 2x với x ∈ [0; 3], có đồ thị như hình 1.15. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/04/blobid2-1712305735.png)
a) Giá trị lớn nhất M của hàm số trên đoạn [0; 3] là bao nhiêu? Tìm x0 sao cho f(x0) = M.
Cho hàm số y = f(x) = x2 – 2x với x ∈ [0; 3], có đồ thị như hình 1.15.
![Cho hàm số y = f(x) = x^2 – 2x với x ∈ [0; 3], có đồ thị như hình 1.15. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/04/blobid2-1712305735.png)
a) Giá trị lớn nhất M của hàm số trên đoạn [0; 3] là bao nhiêu? Tìm x0 sao cho f(x0) = M.
Câu 7:
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:
a) y = x4 – 2x2 + 3;
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:
a) y = x4 – 2x2 + 3;
Câu 8:
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
d) y = (x2 – x)ex trên đoạn [0; 1].
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
d) y = (x2 – x)ex trên đoạn [0; 1].
Câu 9:
b) Giá trị nhỏ nhất m của hàm số trên đoạn [0; 3] là bao nhiêu? Tìm x0 sao cho f(x0) = m.
b) Giá trị nhỏ nhất m của hàm số trên đoạn [0; 3] là bao nhiêu? Tìm x0 sao cho f(x0) = m.
Câu 10:
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
a) y = 2x3 – 6x + 3 trên đoạn [−1; 2];
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:
a) y = 2x3 – 6x + 3 trên đoạn [−1; 2];
Câu 11:
b) Đạo hàm N'(t) biểu thị tốc độ lây lan của vius (còn gọi là tốc độ truyền bệnh). Hỏi virus sẽ lây lan nhanh nhất khi nào?
b) Đạo hàm N'(t) biểu thị tốc độ lây lan của vius (còn gọi là tốc độ truyền bệnh). Hỏi virus sẽ lây lan nhanh nhất khi nào?
Câu 12:
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:
a) ;
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:
a) ;Câu 13:
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:
c) y = xlnx;
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:
c) y = xlnx;
Câu 14:
c) Tính giá trị của hàm số tại hai đầu mút của đoạn [−1; 2] và tại các điểm x đã tìm ở câu b. So sánh số nhỏ nhất trong các giá trị này với , số lớn nhất trong các giá trị này với .
c) Tính giá trị của hàm số tại hai đầu mút của đoạn [−1; 2] và tại các điểm x đã tìm ở câu b. So sánh số nhỏ nhất trong các giá trị này với , số lớn nhất trong các giá trị này với .

