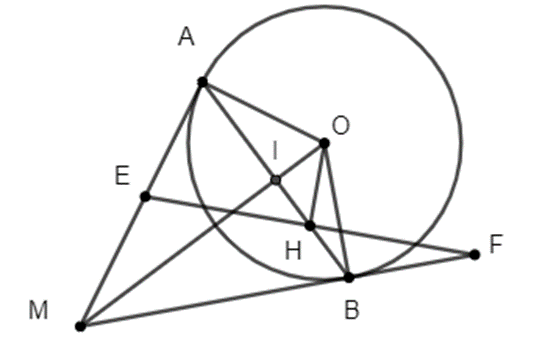
Từ một điểm M ở ngoài đường tròn tâm O vẽ hai tiếp tuyến MA, MB với đường tròn (A, B là hai tiếp điểm). Trên đoạn thẳng AB lấy điểm H (H khác A, B). Qua H kẻ đường thẳng vuông góc với OH cắt đường thẳng MA ở E, cắt đường thẳng MB ở F.
a) Chứng minh tứ giác có bốn đỉnh O, H, A, E là tứ giác nội tiếp.
b) Chứng minh tam giác OEF cân.
c) Kẻ OI vuông góc AB ( I thuộc AB). Chứng minh OI.OF = OB.OH
a) Ta có: MA là tiếp tuyến của (O) nên:
MA\( \bot \)OA.
Mà OH\( \bot \)EF \( \Rightarrow \widehat {EAO} = \widehat {EHO} = 90^\circ \)
Suy ra O, H, A, E cùng thuộc một đường tròn (đpcm).
b) Tương tự câu a) ta có: tứ giác OHFB nội tiếp.
\( \Rightarrow \widehat {OEH} = \widehat {OAH} = \widehat {OAB} = \widehat {OBA} = \widehat {OBH} = \widehat {OFH}\)
Suy ra \(\Delta OEF\) cân tại O.
c) Theo câu a) ta có: \(\widehat {HFO} = \widehat {IBO};\,\,\widehat {OHF} = \widehat {OIB} = 90^\circ \)
\( \Rightarrow \Delta OHF\) ᔕ \(\Delta OIB\) (g.g)
\( \Rightarrow \frac{{OH}}{{OI}} = \frac{{OF}}{{OB}} \Rightarrow OI.OF = OB.OH\).