Từ một điểm A nằm ngoài đường tròn (O) kẻ hai tiếp tuyến AB AC (B và C là hai tiếp điểm). Kẻ đường kính CD của đường tròn (O).

a) Chứng minh OA ⊥ BC.

b) Chứng minh: BD // OA.

c) Kẻ BH ⊥ CD. Gọi K là giao điểm của BH và AD. Chứng minh K là trung điểm của BH.

Lời giải

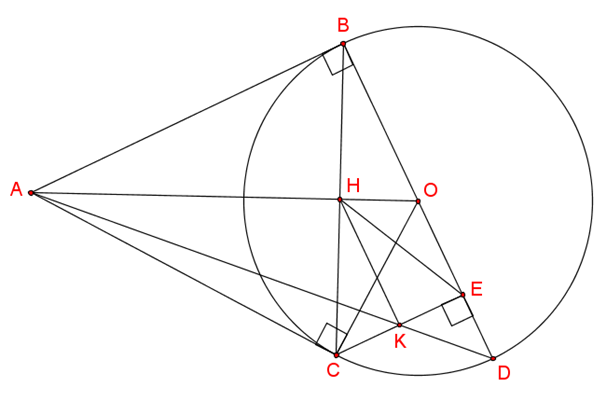
a) Ta có OB = OC (=R).

Suy ra O thuộc đường trung trực của đoạn thẳng CB.

Ta có AB = AC (tính chất hai tiếp tuyến cắt nhau) 

Suy ra A thuộc đường trung trực của đoạn thẳng BC.

Như vậy A, O thuộc đường trung trực của BC suy ra AO ⊥ BC (đpcm)

b) Ta có $\widehat {CBD}$ = 90° (góc nội tiếp chắn nửa đường tròn)

⇒ BD ⊥ BC mà AO ⊥ BC (chứng minh trên)

⇒ BD // AO (đpcm)

c) Ta có KH // AC (vì cùng vuông góc CD).

Theo định lý Ta-let, ta có:

$\frac{{{\rm{KH}}}}{{{\rm{AC}}}}{\rm{ = }}\frac{{{\rm{DH}}}}{{{\rm{DC}}}} \Rightarrow {\rm{KH = }}\frac{{{\rm{DH}}\,{\rm{.}}\,{\rm{AC}}}}{{{\rm{DC}}}}$ (1)

Xét ΔACO và ΔBHD có: $\widehat {ACO} = \widehat {BHD} = 90^\circ$

$\widehat {ACO} = \widehat {BDO}$ (hai góc đồng vị, BD // AO)

⇒ ∆ACO ᔕ ∆BHD (g.g)

⇒ $\frac{{AC}}{{BH}} = \frac{{CO}}{{HD}} \Rightarrow BH = \frac{{AC.HD}}{{CO}}$          (2)

Từ (1) và (2) ta có: $\frac{{KH}}{{BH}} = \frac{{CO}}{{DC}} = \frac{1}{2}$.

Vậy BK = KH, K là trung điểm cạnh BH (đpcm).