Từ điểm A nằm ngoài đường tròn (O), vẽ tiếp tuyến AB đến (O) (B là tiếp điểm). Vẽ BE là đường kính của (O). Dựng đường cao BC của ∆OAB, tia BC cắt (O) tại D (D khác B).

a) Chừng minh AD là tiếp tuyến của (O) và OA // DE.

b) Gọi F là giao điểm của AE và (O) (F khác E). Chứng minh AE . AF = AC . AO.

c) Gọi G là giao điểm của BF và ED, H là giao điểm của AE và BD, I là giao điểm của AB và DE. Chứng minh GH // AB và AB = AI.

Lời giải

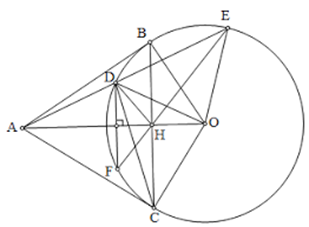
a) Ta có: OB = OD (= R) nên ∆ODB cân tại O.

Mà OC là đường cao của ∆ODB.

Nên OC cũng là đường phân giác của ∆ODB.

⇒ $\widehat {BOC} = \widehat {COD}$ hay $\widehat {BOA} = \widehat {AOD}$.

Xét ∆ABO và ∆ADO có:

OB = OD (= R)

$\widehat {BOA} = \widehat {AOD}$ (chứng minh trên)

Cạnh OA chung

Do đó ∆ABO = ∆ADO (c.g.c)

Suy ra $\widehat {ABO} = \widehat {ADO} = 90^\circ$.

Do đó AD là tiếp tuyến của (O).

Ta có: $\widehat {DEB} = \frac{1}{2}$ sđ  (1)

Lại có: $\widehat {BOD}$ = sđ

Mà $\widehat {BOA}$ = $\frac{1}{2}$$\widehat {BOD}$

Nên $\widehat {BOA}$ = $\frac{1}{2}$ sđ          (2)

Từ (1) và (2) suy ra $\widehat {BOA} = \widehat {DEO}$.

Mà hai góc này nằm ở vị trí đồng vị nên OA // DE.

b) Vì F thuộc đường tròn đường kính BE nên $\widehat {BFE} = 90^\circ$

Xét ∆ABE vuông tại B có: BF là đường cao

Suy ra AE . AF = AB²

Chứng minh tương tự, ta có: AC . AO = AD².

Mà AB = AD (tính chất hai tiếp tuyến cắt nhau)

Do đó AB² = AD²

Suy ra: AE . AF = AC.AO.

c) Vì D thuộc đường tròn đường kính BE nên $\widehat {BDE} = 90^\circ$.

Ta có: BD là đường cao của ∆BGE; EF là đường cao của ∆BGE.

Mà BD, EF cắt nhau tại H.

Do đó H là trực tâm của ∆BGE.

Suy ra: GH ⊥ BE; AB ⊥ BE

Nên GH // AB.

Xét ∆BIE có: BO = EO (= R); AO // EI (AO // DE).

Do đó AB = AI.