Trong tất cả các hình chóp tứ giác đều nội tiếp mặt cầu có bán kính bằng 9. Khối chóp có thể tích lớn nhất bằng bao nhiêu?

Gọi I là tâm mặt cầu và S.ABCD là hình chóp nội tiếp mặt cầu.

Gọi X là độ dài cạnh SO, M là trung điểm của SD

Ta có: $\text{SI}.\text{SO}=\text{SM}.\text{SD}=\frac{1}{2}{\text{SD}}^2\Rightarrow {\text{SD}}^2=2\text{SI}.\text{SO}=18\text{x}$ 

Suy ra ${\text{OD}}^2=18\text{x}-{\text{x}}^2$

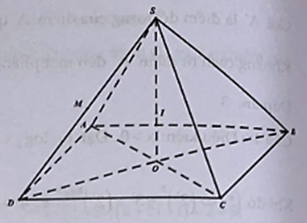
Thế tích khối chóp S.ABCD bằng

$V=\frac{1}{3}SO{S}_{ABCD}=\frac{1}{3}x\mathrm{.2.}O{D}^2=\frac{2}{3}x\left(18x-x^2\right)=\frac{2}{3}{x}^2(18-x)$

Ta có: $x^2(18-x)=4\frac{x}{2}.\frac{x}{2}(18-x)\le 4.{\left(\frac{18}{3}\right)}^3=864$ 

Vậy thể tích của khối chóp là: $\text{V}=\frac{2}{3}.864=576$