Trong mặt phẳng tọa độ Oxy, cho đường thẳng (d₁): y = –x + 2 và (d₂): \(y = \frac{1}{4}x\).

1) Vẽ (d₁) và (d₂) trên cùng hệ trục tọa độ Oxy.

2) Lấy điểm B trên (d₂) có hoành độ bằng –4. Viết phương trình đường thẳng (d₃) song song với (d₁) và qua điểm B.

3) Tìm tọa độ giao điểm của (d₁) và (d₂) bằng phép tính.

Lời giải

1) Bảng giá trị của (d₁):

Bảng giá trị của (d₂):

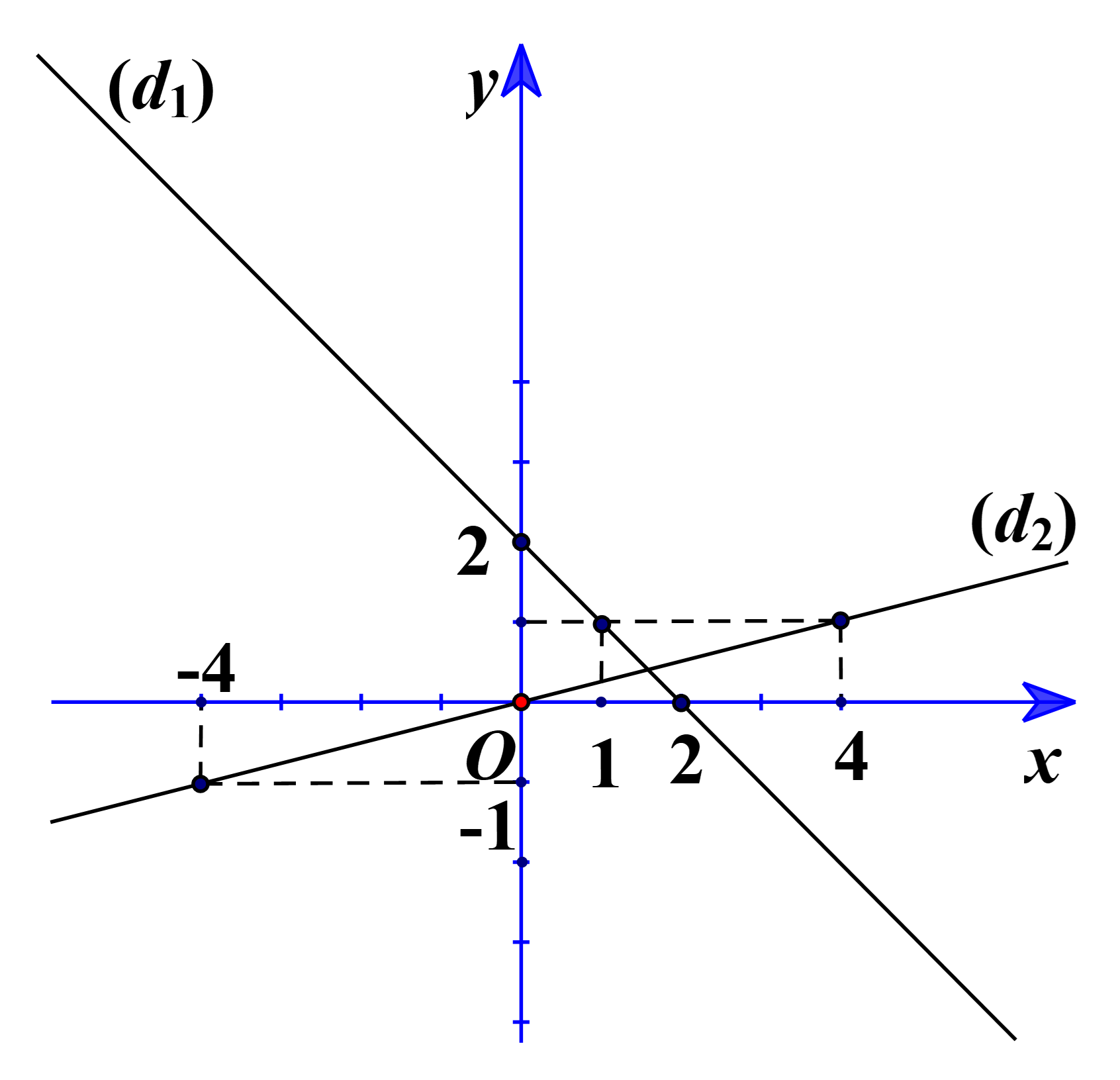
2) Gọi B(–4; y_B).

Ta có B(–4; y_B) ∈ (d₂).

Suy ra \(y = \frac{1}{4}.\left( { - 4} \right) = - 1\).

Do đó tọa độ B(–4; –1).

Vì (d₃) // (d₁) nên phương trình (d₃) có dạng: y = –x + m (m ≠ 2).

Ta có B(–4; –1) ∈ (d₃).

Suy ra –1 = 4 + m.

Do đó m = –5 (nhận)

Vậy phương trình (d₃): y = –x – 5.

3) Phương trình hoành độ giao điểm của (d₁) và (d₂): \( - x + 2 = \frac{1}{4}x\).

\( \Leftrightarrow \frac{5}{4}x = 2\)

\( \Leftrightarrow x = \frac{8}{5}\).

Với \(x = \frac{8}{5}\), ta có: \(y = - \frac{8}{5} + 2 = \frac{2}{5}\).

Vậy giao điểm của (d₁) và (d₂) là điểm \(E\left( {\frac{8}{5};\frac{2}{5}} \right)\).