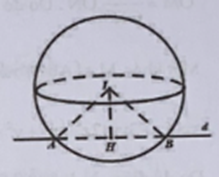
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d x - 1/ -1 = y/ 2 = z + 3/ -1 và mặt cầu (S) tâm I có phương trình
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d:x−1−1=y2=z+3−1 và mặt cầu (S) tâm I có phương trình (S):(x−1)2+(y−2)2+(z+1)2=18. Đường thẳng d cắt (S) tại hai điểm A, B. Tính diện tích tam giác IAB.
A. 8√113
B. 16√113
C. √116
D. 8√119