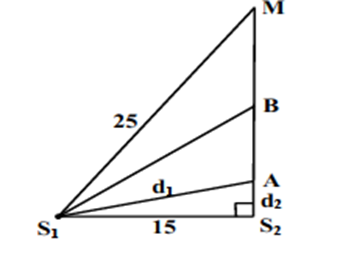
Trên mặt chất lỏng, có hai nguồn kết hợp S₁ và S₂ cách nhau 15 cm, dao động theo phương thẳng đứng với phương trình là \({u_{S1}} = {u_{S2}} = 2\cos \left( {10\pi t - \frac{\pi }{4}} \right)\) (cm). Tốc độ truyền sóng trên mặt chất lỏng là 20 cm/s. Coi biên độ sóng không đổi khi truyền đi. Trên đường thẳng vuông góc với \({S_1}{S_2}\) tại \({S_2}\) lấy điểm M sao cho \(M{S_1} = 25cm\) và \(M{S_2} = 20\) cm. Điểm A và B lần lượt nằm trong đoạn \({S_2}M\) với A gần \({S_2}\) nhất, B xa \({S_2}\) nhất, đều có tốc độ dao động cực đại bằng 40π cm/s. Khoảng cách AB là

D. 13,55 cm.

Chọn A. \[\lambda = \frac{v}{f} = \frac{{20}}{5} = 4\]cm. Hai nguồn cùng pha.

Điểm A và B có tốc độ dao động \[\user2{v = 40\pi cm/s = \omega }\user2{.2A = }{\user2{v}_{max}}\]nên điểm A và B là các điểm dao động với biên độ cực đại, nên ta có:

Trên đoạn \({S_2}M\)ta có: \[\frac{{\user2{M}{\user2{S}_\user2{1}}\user2{ - M}{\user2{S}_\user2{1}}}}{\user2{\lambda }}\user2{ < k < }\frac{{{\user2{S}_\user2{1}}{\user2{S}_\user2{2}}}}{\user2{\lambda }}\user2{ = > }\]\[\frac{{\user2{25 - 20}}}{4}\user2{ < k < }\frac{{\user2{15}}}{4}\user2{ = > }\]\[\user2{1,25 < k < 3,75}\]

=>Chọn k=2;3.

 Trên hình vẽ \[M{{\rm{S}}_2} \bot {{\rm{S}}_1}{{\rm{S}}_2}\], ta có: \[d_1^2 - d_2^2 = S_1^{}S_2^2\]

=> \[\left\{ \begin{array}{l}\user2{d}_\user2{1}^{}\user2{ - d}_\user2{2}^{}\user2{ = k\lambda }\\\user2{d}_\user2{1}^{}\user2{ + d}_\user2{2}^{}\user2{ = }\frac{{{\user2{S}_\user2{1}}\user2{S}_\user2{2}^\user2{2}}}{{\user2{k\lambda }}}\end{array} \right.\user2{ = > d}_\user2{2}^{}\user2{ = }\frac{{{\user2{S}_\user2{1}}\user2{S}_\user2{2}^\user2{2}}}{{\user2{2k\lambda }}}\user2{ - }\frac{{\user2{k\lambda }}}{\user2{2}} = \frac{{\user2{15}_{}^\user2{2}}}{{\user2{8k}}}\user2{ - 2k}\].

=>\[\left\{ \begin{array}{l}\user2{k = 2 = > d}_\user2{2}^{} = \frac{{\user2{15}_{}^\user2{2}}}{{\user2{8}\user2{.2}}}\user2{ - 2}\user2{.2 = 10,0625}\;\user2{cm}\\\user2{k = 3 = > d}_\user2{2}^{} = \frac{{\user2{15}_{}^\user2{2}}}{{\user2{8}\user2{.3}}}\user2{ - 3}\user2{.2 = 3,375}\;\user2{cm}\end{array} \right.\]

ð    AB=10,0625 -3,375 =6,6875 cm.