Tìm m để phương trình sau có 3 nghiệm phân biệt: x³ − 6x² + 3(m + 2)x − m − 6 = 0.

x³ − 6x² + 3(m + 2)x − m − 6 = 0

<=> x³ − 6x² + 3mx + 6x − m − 6 = 0

<=> x³ − 6x² + 6x − 6 = m(1 − 3x) (1)

• TH1: 1 − 3x = 0 $\iff x=\frac{1}{3}$

Khi đó, phương trình (*) trở thành $-\frac{125}{27}=m.0$ (vô nghiệm).

• TH2: 1 ≠ 3x = 0 $\iff x\ne \frac{1}{3}$

Khi đó, phương trình (1) trở thành $m=\frac{x^3-6x^2+6x-6}{1-3x}=f\left(x\right)$ (*)

Số nghiệm của phương trình (*) là số giao điểm của đồ thị hàm số y = f (x) và đường thẳng y = m.

Ta có: 

$$\begin{gathered} f^{\text{'}}\left(x\right)=\frac{\left(3x^2-12x+6\right)\left(1-3x\right)+3\left(x^3-6x^2+6x-6\right)}{{\left(1-3x\right)}^2} \\ \Rightarrow f^{\text{'}}\left(x\right)=\frac{-6x^3+21x^2-12x-12}{{\left(1-3x\right)}^2}=0 \\ \Rightarrow -6x^3+21x^2-12x-12=0 \end{gathered}$$

<=> 2x³ − 7x² + 4x + 4 = 0

<=> (2x + 1)(x − 2)² = 0

$\Rightarrow \left[\begin{array}{l}x=\frac{-1}{2}\\ x=2\end{array}\right.$

Ta có BBT:

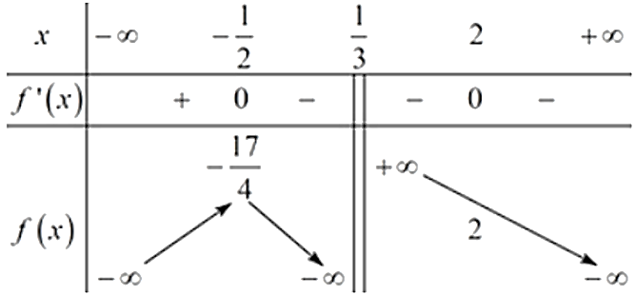
Dựa vào BBT ta thấy phương trình (*) có 2 nghiệm phân biệt khi và chỉ khi $m=-\frac{17}{4}.$