Tìm giá trị nhỏ nhất của hàm số y = 3x + 4/x^2 trên khoảng (0; + vô cùng)
Tìm giá trị nhỏ nhất của hàm số \(y = 3x + \frac{4}{{{x^2}}}\) trên khoảng (0; +∞).
Ta có: \(y' = 3 - \frac{8}{{{x^3}}}\) ⇒ \(y' = 0\) ⇔ \(3 - \frac{8}{{{x^3}}} = 0\) ⇔ \({x^3} = \frac{8}{3}\) ⇔ \(x = \frac{2}{{\sqrt[3]{3}}}\)
Hàm số y có bảng biến thiên sau:
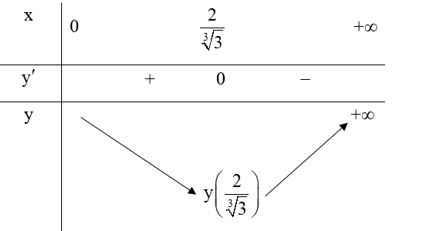
Nhìn vào bảng biến thiên ta thấy giá trị nhỏ nhất của hàm số y trên khoảng (0; +∞) là \(y\left( {\frac{2}{{\sqrt[3]{3}}}} \right)\) ⇒ \(\mathop {\min y}\limits_{\left( {0; + \infty } \right)} = 3.\frac{2}{{\sqrt[3]{3}}} + \frac{4}{{{{\left( {\frac{2}{{\sqrt[3]{3}}}} \right)}^2}}} = 3\sqrt[3]{9}.\)
Vậy giá trị nhỏ nhất của hàm số y trên khoảng (0; +∞) là \(3\sqrt[3]{9}.\)