Tìm giá trị nhỏ nhất của biểu thức $A=\frac{\left({\text{x}}^3+y^3\right)-\left(x^2+y^2\right)}{\left(x-1\right)\left(y-1\right)}$  với x, y là các số thực lớn hơn 1.

Ta có

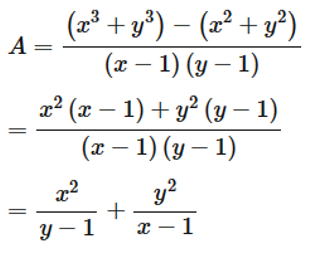
Theo bất đẳng thức Cô – si ta có

$\frac{x^2}{y-1}+4\left(y-1\right)\ge 2\sqrt{\frac{x^2}{y-1}.4\left(y-1\right)}=4\text{x}$

$\frac{y^2}{x-1}+4\left(x-1\right)\ge 2\sqrt{\frac{y^2}{x-1}.4\left(x-1\right)}=4y$

Suy ra $\frac{x^2}{y-1}+\frac{y^2}{x-1}+4\left(y-1\right)+4\left(\text{x}-1\right)\ge 4\text{x + 4y}$

$\iff \frac{x^2}{y-1}+\frac{y^2}{x-1}\ge 8$

Hay A ≥ 8

Dấu “ = ” xảy ra khi $\left\{\begin{array}{l}x=2\left(y-1\right)\\ y=2\left(x-1\right)\end{array}\right.\iff \left\{\begin{array}{l}x-2y=-2\\ y-2\text{x}=-1\end{array}\right.\iff \left\{\begin{array}{l}x=2\\ y=2\end{array}\right.$

Vậy giá trị nhỏ nhất của A bằng khi x = y = 2.