Câu hỏi:
09/04/2024 31
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:
a) trên nửa khoảng [2; +∞);
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:
a) trên nửa khoảng [2; +∞);
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
a) trên nửa khoảng [2; +∞)
Có
Do đó và hàm số không có giá trị nhỏ nhất trên nửa khoảng [2; +∞).
a) trên nửa khoảng [2; +∞)
Có
Do đó và hàm số không có giá trị nhỏ nhất trên nửa khoảng [2; +∞).
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Dân số của một quốc gia sau t (năm) kể từ năm 2023 được ước tính bởi công thức: N(t) = 100e0,012t (N(t) được tính bằng triệu người, 0 ≤ t ≤ 50).
a) Ước tính dân số của quốc gia này vào các năm 2030 và 2035 (kết quả tính bằng triệu người, làm tròn kết quả đến chữ số thập phân thứ ba).
Dân số của một quốc gia sau t (năm) kể từ năm 2023 được ước tính bởi công thức: N(t) = 100e0,012t (N(t) được tính bằng triệu người, 0 ≤ t ≤ 50).
a) Ước tính dân số của quốc gia này vào các năm 2030 và 2035 (kết quả tính bằng triệu người, làm tròn kết quả đến chữ số thập phân thứ ba).
Câu 2:
Tiệm cận xiên của đồ thị hàm số là
A. y = −2. B. y = 1. C. y = x + 2. D. y = x.
Tiệm cận xiên của đồ thị hàm số là
A. y = −2. B. y = 1. C. y = x + 2. D. y = x.
Câu 3:
c) Đạo hàm của hàm số N(t) biểu thị tốc độ tăng dân số của quốc gia đó (tính bằng triệu người/năm). Vào năm nào tốc độ tăng dân số của quốc gia đó là 1,6 triệu người/năm.
c) Đạo hàm của hàm số N(t) biểu thị tốc độ tăng dân số của quốc gia đó (tính bằng triệu người/năm). Vào năm nào tốc độ tăng dân số của quốc gia đó là 1,6 triệu người/năm.
Câu 4:
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:
b) .
Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của các hàm số sau:
b) .
Câu 5:
Xét chiều biến thiên và tìm các cực trị (nếu có) của các hàm số sau:
c) ;
Xét chiều biến thiên và tìm các cực trị (nếu có) của các hàm số sau:
c) ;Câu 6:
Xét chiều biến thiên và tìm các cực trị (nếu có) của các hàm số sau:
a) y = x3 – 3x2 + 3x – 1;
Xét chiều biến thiên và tìm các cực trị (nếu có) của các hàm số sau:
a) y = x3 – 3x2 + 3x – 1;Câu 7:
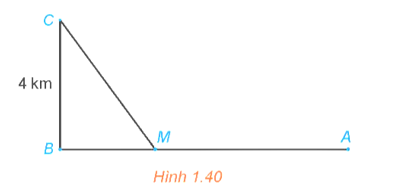
Một đường dây điện được nối từ một nhà máy điện ở A đến một hòn đảo ở C như Hình 1.40. Khoảng cách từ C đến B là 4 km. Bờ biển chạy thẳng từ A đến B với khoảng cách là 10 km. Tổng chi phí lắp đặt cho 1 km dây điện trên biển là 50 triệu đồng, còn trên đất liền là 30 triệu đồng. Xác định vị trí điểm M trên đoạn AB (điểm nối dây từ đất liền ra đảo) để tổng chi phí lắp đặt là nhỏ nhất.
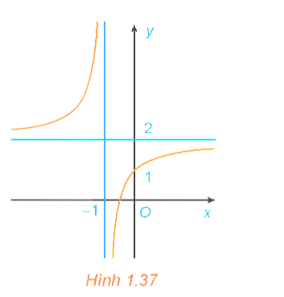
Câu 8:
Cho hàm số y = f(x) xác định trên ℝ\{1; 3}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau
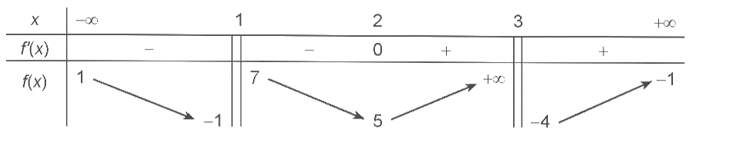
Khẳng định nào sau đây là sai?
A. Đường thẳng y = 1 là tiệm cận ngang của đồ thị hàm số đã cho.
B. Đường thẳng y = −1 là tiệm cận ngang của đồ thị hàm số đã cho.
C. Đường thẳng x = 3 là tiệm cận đứng của đồ thị hàm số đã cho.
D. Đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số đã cho.
Cho hàm số y = f(x) xác định trên ℝ\{1; 3}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau

Khẳng định nào sau đây là sai?
A. Đường thẳng y = 1 là tiệm cận ngang của đồ thị hàm số đã cho.
B. Đường thẳng y = −1 là tiệm cận ngang của đồ thị hàm số đã cho.
C. Đường thẳng x = 3 là tiệm cận đứng của đồ thị hàm số đã cho.
D. Đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số đã cho.
Câu 13:
Cho hàm số y = f(x) thỏa mãn: và . Khẳng định nào sau đây là đúng?
A. Đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số.
B. Đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số.
C. Đường thẳng y = 1 là tiệm cận ngang của đồ thị hàm số.
D. Đường thẳng x = 2 là tiệm cận ngang của đồ thị hàm số.
Cho hàm số y = f(x) thỏa mãn: và . Khẳng định nào sau đây là đúng?
A. Đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số.
B. Đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số.
C. Đường thẳng y = 1 là tiệm cận ngang của đồ thị hàm số.
D. Đường thẳng x = 2 là tiệm cận ngang của đồ thị hàm số.
Câu 14:
Xét một thấu kính hội tụ có tiêu cự f (H.1.39). Khoảng cách p từ vật đến thấu kính liên hệ với khoảng cách q từ ảnh đến thấu kính bởi hệ thức: .
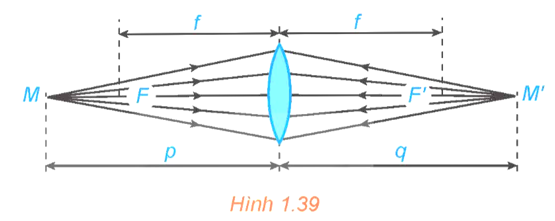
a) Viết công thức tính q = g(p) như một hàm số của biến p ∈ (f; +∞).
Xét một thấu kính hội tụ có tiêu cự f (H.1.39). Khoảng cách p từ vật đến thấu kính liên hệ với khoảng cách q từ ảnh đến thấu kính bởi hệ thức: .

a) Viết công thức tính q = g(p) như một hàm số của biến p ∈ (f; +∞).
Câu 15:
Giá trị lớn nhất của hàm số y = (x – 2)2ex trên đoạn [1; 3] là
A. 0. B. e3. C. e4. D. e.
Giá trị lớn nhất của hàm số y = (x – 2)2ex trên đoạn [1; 3] là
A. 0. B. e3. C. e4. D. e.