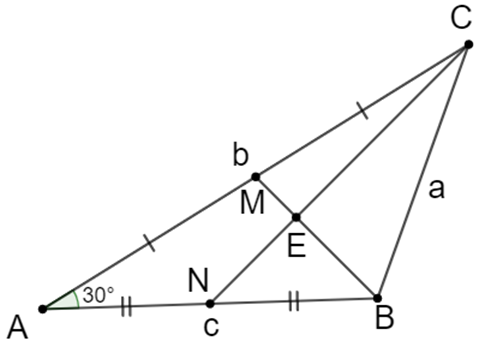
Gọi E là giao điểm của BM và CN.

Ta có công thức đường trung tuyến:

$$\begin{gathered} C{N}^2=\frac{C{A}^2+C{B}^2}{2}-\frac{A{B}^2}{4}=\frac{b^2+a^2}{2}-\frac{c^2}{4} \\ \Rightarrow C{E}^2=\frac{4}{9}C{N}^2=\frac{4}{9}\left(\frac{b^2+a^2}{2}-\frac{c^2}{4}\right) \\ B{M}^2=\frac{B{A}^2+B{C}^2}{2}-\frac{C{A}^2}{4}=\frac{c^2+a^2}{2}-\frac{b^2}{4} \\ \Rightarrow B{E}^2=\frac{4}{9}B{M}^2=\frac{4}{9}\left(\frac{c^2+a^2}{2}-\frac{b^2}{4}\right) \end{gathered}$$

Trong tam giác ABC có: BM $\perp$ CN nên tam giác CEB vuông tại E

=> CE² + BE² = BC²

^{$$\begin{gathered} \Rightarrow \frac{4}{9}\left(\frac{b^2+a^2}{2}-\frac{c^2}{4}\right)+\frac{4}{9}\left(\frac{c^2+a^2}{2}-\frac{b^2}{4}\right)=a^2 \\ \iff \frac{1}{9}{b}^2+\frac{1}{9}{c}^2+\frac{4}{9}{a}^2=a^2 \\ \iff 5a^2=b^2+c^2 \end{gathered}$$}

Tam giác ABC có:

a² = b² + c² − 2bc.cos A = 5a² − 2bc.cos A

$\Rightarrow bc=\frac{2a^2}{\cos A}$

Khi đó: $S=\frac{1}{2}bc.\sin A=\frac{1}{2}.\frac{2a^2}{\cos A}.\sin A=a^2.\tan A=a^2.\tan 30°=3\sqrt{3}$