Tam giác ABC có hai đường trung tuyến BM, CN vuông góc với nhau và có

Trả lời

Xét bài toán: Tam giác ABC, điều kiện cần và đủ để hai trung tuyến kẻ từ B và C vuông góc với nhau là: $b^2+c^2=5a^2.$

Ta có: Gọi G là giao điểm của hai trung tuyến BM, CN. Áp dụng công thức trung tuyến ta có:

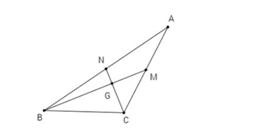
$G{B}^2=\frac{4}{9}B{M}^2=\frac{1}{9}(2a^2+2c^2-b^2);G{C}^2=\frac{4}{9}C{N}^2=\frac{1}{9}(2a^2+2b^2-c^2)$

Áp dụng định lý Pythago cho tam giác vuông BGC, ta có: $B{G}^2+C{G}^2=B{C}^2$

Khi đó ta có: $\frac{1}{9}(2a^2+2c^2-b^2)+\frac{1}{9}(2a^2+2b^2-c^2)=a^2\iff 4a^2+b^2+c^2=9a^2\iff b^2+c^2=5a^2.$

Quay trở lại bài toán trên, xét tam giác ABC ta có:

$a^2=b^2+c^2-2bc.\cos A=5a^2-2bc.\cos A\Rightarrow bc=\frac{2a^2}{\cos A}.$

Khi đó: $S=\frac{1}{2}bc.\sin A=\frac{1}{2}\frac{2a^2}{\cos A}.\sin A=a^2\tan A=3\sqrt{3}.$