Tam giác ABC có AB = 3, AC = 6, góc BAC = 60^. Tính độ dài đường cao HA của tam giác.

Trả lời

Lời giải

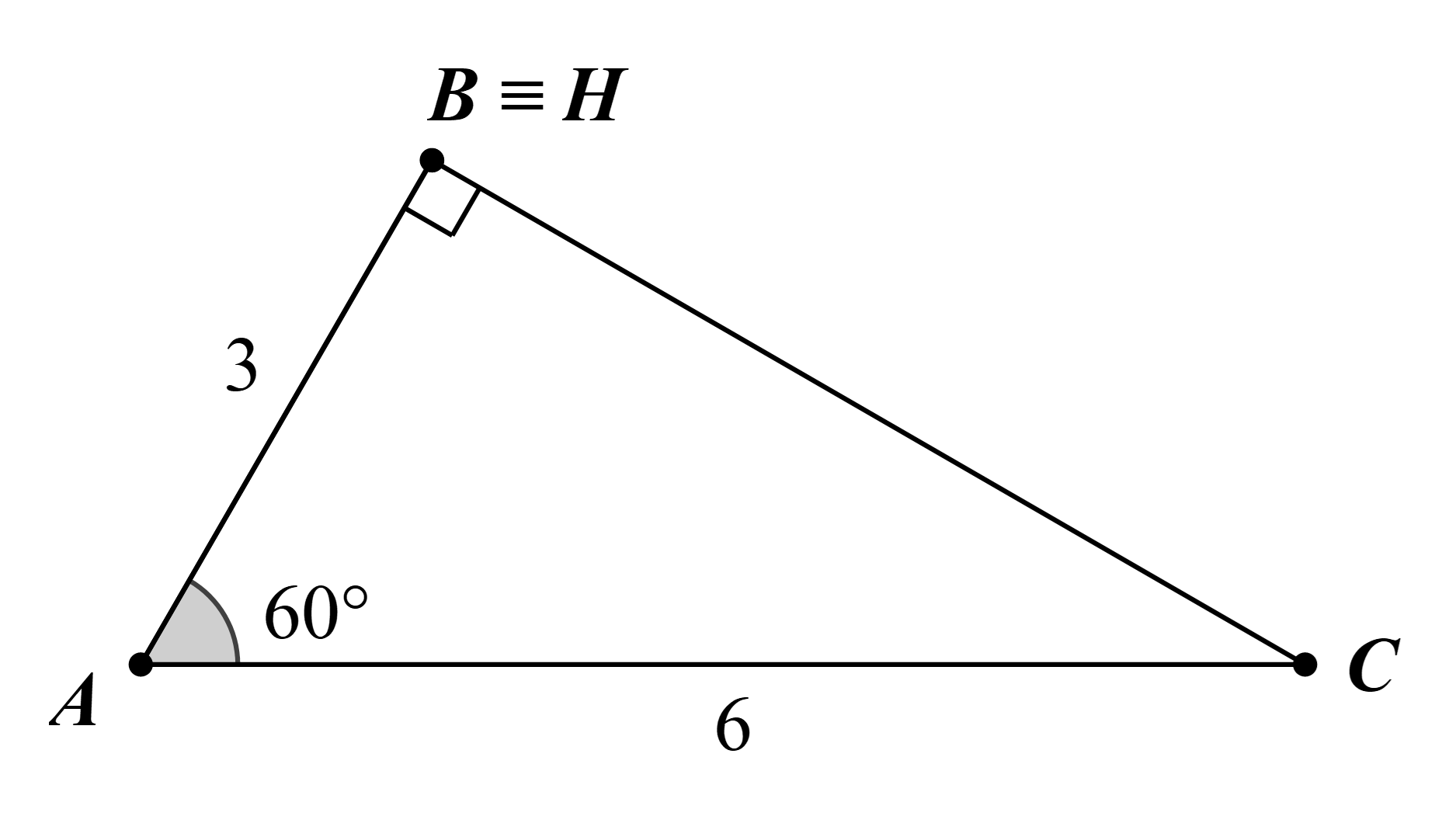
BC² = AB² + AC² – 2.AB.AC.cos$\widehat {BAC}$.

= 9 + 36 – 2.3.6.cos60°

= 27.

Suy ra $BC = 3\sqrt 3$.

$\cos \widehat {ABC} = \frac{{A{B^2} + B{C^2} - A{C^2}}}{{2.AB.BC}} = \frac{{9 + 27 - 36}}{{2.3.3\sqrt 3 }} = 0$.

Suy ra $\widehat {ABC} = 90^\circ$.

Do đó tam giác ABC vuông tại A.

Vì vậy B ≡ H.

Vậy AH = AB = 3.