Số các giá trị nguyên của tham số m để phương trình ${\log }_{\sqrt{2}}(x-1)={\log }_2(mx-8)$ có hai nghiệm phân biệt là

Ta có ${\log }_{\sqrt{2}}(x-1)={\log }_2(\text{mx}-8)\iff 2{\log }_2(\text{x}-1)={\log }_2(\text{mx}-8)$

$\iff \left\{\begin{array}{l}x>1\\ {\log }_2{(x-1)}^2={\log }_2(mx-8)\end{array}\iff \left\{\begin{array}{l}x>1\\ {(x-1)}^2=mx-8\end{array}\iff \left\{\begin{array}{l}x>1\\ m=x-2+\frac{9}{x}\end{array}\right.\right.\right.$

Xét hàm số $\text{f}\left(\text{x}\right)=\text{x}-2+\frac{9}{\text{x}}$ với x > 1. Ta có ${\text{f}}^{\text{'}}\left(\text{x}\right)=1-\frac{9}{{\text{x}}^2}=0\iff \text{x}=3$ (do x > 1.

Bảng biến thiên

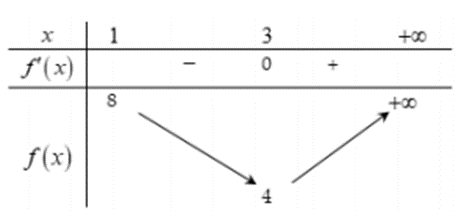
Phương trình đã cho có hai nghiệm phân biệt khi và chỉ khi 4 < m < 8.