Qua điểm M nằm ngoài (O), vẽ tiếp tuyến MA (A là tiếp điểm) và cát tuyến MBC (tia MO nằm giữa hai tia MA và MB).

a) Chứng minh MA² = MB.MC.

b) Kẻ AH vuông góc với OM tại H. Chứng minh MH.MO = MB.MC và tứ giác OHBC nội tiếp.

c) Tia BH cắt (O) tại điểm thứ hai là K. Chứng minh C đối xứng K qua đường thẳng OM.

Lời giải

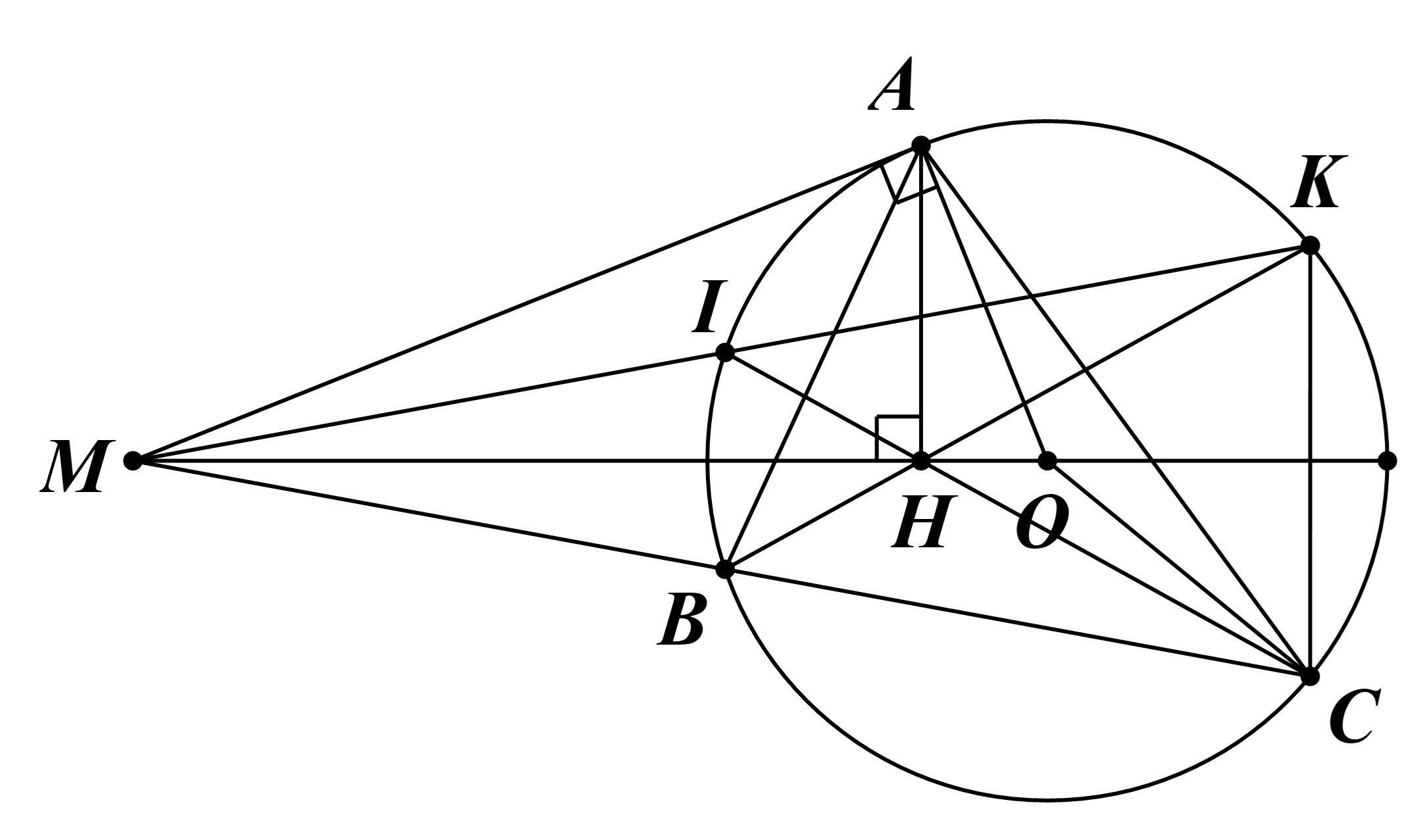
a) Xét ∆ABM và ∆CAM, có:

$\widehat M$ chung;

$\widehat {MAB} = \widehat {MCA}$ (góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung).

Do đó  (g.g).

Suy ra $\frac{{AM}}{{CM}} = \frac{{BM}}{{AM}}$.

Vậy MA² = MB.MC (điều phải chứng minh).

b) Ta có MA là tiếp tuyến của (O).

Suy ra $\widehat {MAO} = 90^\circ$.

Tam giác MAO vuông tại A có AH là đường cao:

MA² = MH.MO (hệ thức lượng trong tam giác vuông).

Mà MA² = MB.MC (câu a).

Vậy MH.MO = MB.MC (điều phải chứng minh).

Xét ∆MBH và ∆MOC, có:

$\widehat M$ chung;

$\frac{{MH}}{{MC}} = \frac{{MB}}{{MO}}$ (do MH.MO = MB.MC).

Do đó  (c.g.c).

Suy ra $\widehat {MBH} = \widehat {MOC}$ (cặp góc tương ứng).

Vậy tứ giác OHBC cùng thuộc một đường tròn.

c) Gọi I là giao điểm của Mk và (O).

Ta có $\widehat {CBK} = \widehat {CIK}$ (cùng chắn ).

Mà $\widehat {MBK} + \widehat {KBC} = 180^\circ$ và $\widehat {MIC} + \widehat {CIK} = 180^\circ$.

Suy ra $\widehat {MBK} = \widehat {MIC}$.

Xét ∆MIC và ∆MBK, có:

$\widehat M$ chung;

$\widehat {MBK} = \widehat {MIC}$ (chứng minh trên).

Do đó  (g.g).

Suy ra $\frac{{MI}}{{MB}} = \frac{{MC}}{{MK}} = \frac{{IC}}{{BK}}$

$\Leftrightarrow \frac{{MI}}{{MB}} = \frac{{MC}}{{IC}} = \frac{{MK}}{{BK}}$

$\Leftrightarrow \frac{{MI}}{{MK}} = \frac{{BK}}{{IC}} = \frac{{MB}}{{MC}}$.

Xét ∆MIB và ∆MKC, có:

$\widehat M$ chung;

$\frac{{MI}}{{MK}} = \frac{{MB}}{{MC}}$ (chứng minh trên).

Do đó  (c.g.c).

Suy ra $\widehat {MIB} = \widehat {MKC}$ (cặp góc tương ứng).

Mà hai góc này ở vị trí đồng vị.

Do đó IB // KC.

Vì vậy .

Suy ra $\widehat {ICK} = \widehat {BKC}$.

Do đó tam giác HKC cân tại H.

Vì vậy HK = HC.

Mà OK = OC (= R).

Khi đó HO là đường trung trực của đoạn thẳng KC.

Vậy C đối xứng K qua đường thẳng OM.