A. −16 < m < 16;

B. −18 < m < 14;

C. −14 < m < 18;

D. −4 < m < 4.

Chọn C

$x^3-12x+m-2=0$ <=> $x^3-12x-2=-m$ (1)

Phương trình (1) có 3 nghiệm phân biệt

=> Đường thẳng y = −m cắt đồ thị hàm số y = x³ − 12x − 2 tại 3 điểm phân biệt.

Xét hàm số f (x) = x³ − 12x − 2 => f '(x) = 3x² − 12 = 0

<=> x = ± 2.

Ta có BBT của hàm số f (x) = x³ − 12x − 2 với tập xác định là ℝ

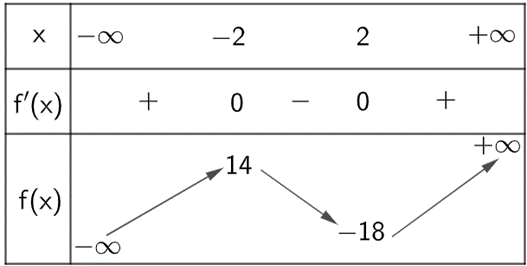
Dựa vào BBT ta có: −18 < −m < 14 <=> −14 < m < 18.