Một vật khối lượng m = 1 kg được kéo chuyển động ngang bởi một lực \(\vec F\) hợp với phương ngang một góc \(\alpha \)= 30° và có độ lớn F = 2 N. Biết khi bắt đầu chuyển động được 2 s vật đi được quãng đường 1,66 m. Cho g = 10 m/s², \(\sqrt 3 = 1,73\).

a, Tính hệ số ma sát trượt giữa vật và mặt sàn.

b, Tính hệ số ma sát với lực kéo nói trên vật chuyển động thẳng đều.

Lời giải

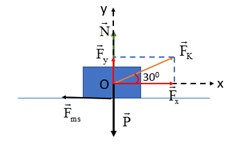
Chọn hệ trục Oxy như hình vẽ.

Vật chịu tác dụng của các lực \(\vec F,\,{\vec F_{ms}},\vec N,\,\vec P\)

Theo định luật II Newton, ta có: \(\vec F + {\vec F_{ms}} + \vec N + \vec P = m.\vec a\)

Chiếu lần lượt lên Ox, Oy, ta được:

\(\left\{ {\begin{array}{*{20}{c}}{{F_x} - {F_{ms}} = m.a \Rightarrow {F_x} - \mu .N = m.a\,(1)}\\{{F_y} + N - P = 0 \Rightarrow N = P - F{}_y\,(2)}\end{array}} \right.\)

Thay (2) vào (1), được:

\(F.cos{30^0} - \mu \left( {P - F.\sin {{30}^0}} \right) = m.a\,\,\left( 3 \right)\)

Lại có: \(s = {v_0}.t + \frac{1}{2}a.{t^2} \Rightarrow a = \frac{{2s}}{{{t^2}}} = \frac{{2.1,66}}{{{2^2}}} = 0,83\,m/{s^2}\)

Thay vào (3) \( \Rightarrow \mu = \frac{{F.cos{{30}^0} - m.a}}{{P - F.\sin {{30}^0}}} = \frac{{2.\frac{{\sqrt 3 }}{2} - 1.0,83}}{{1.10 - 2.0,5}} \approx 0,1\)

b. Khi vật chuyển động thẳng đều thì a = 0

\( \Rightarrow \mu = \frac{{F.cos{{30}^0} - m.a}}{{P - F.\sin {{30}^0}}} = \frac{{2.\frac{{\sqrt 3 }}{2} - 1.0}}{{1.10 - 2.0,5}} \approx 0,192\)