Một vật được ném từ một điểm M ở độ cao h = 45 m với vận tốc ban đầu v_o = 20 m/s lên trên theo phương hợp với phương nằm ngang một góc 45⁰. Lấy g = 10 m/s², bỏ qua lực cản của không khí. Hãy xác định:

a. Quỹ đạo của vật, độ cao cực đại vật đạt đươc so với mặt đất và thời gian vật bay trong không khí.

b. Tầm bay xa của vật, vận tốc của vật khi chạm đất.

c. Xác định thời gian để vật có độ cao 50 m và xác định vận tốc của vật khi đó.

Lời giải

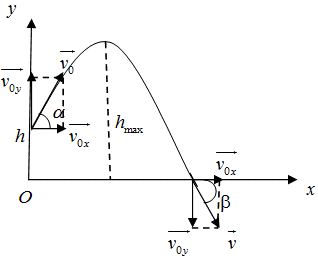
a. Chọn hệ quy chiếu Oxy như hình vẽ, gốc thời gian là lúc khảo sát vật.

Chiếu lên trục ox có:

\[\left\{ \begin{array}{l}\begin{array}{*{20}{c}}{{x_0} = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\\\begin{array}{l}{v_{0x}} = {v_0}.cos\alpha = 20.cos{45^0} = 10\sqrt 2 \left( {m/s} \right)\\{a_x} = 0\end{array}\end{array}\\{v_x} = 10\sqrt 2 \left( {m/s} \right)\end{array} \right.\]

\( \Rightarrow x = 10\sqrt 2 .t\,\,(m)\)

Chiếu lên trục oy có:

\[\left\{ \begin{array}{l}\begin{array}{*{20}{c}}{{y_0} = 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\\\begin{array}{l}{v_{0y}} = {v_0}.\sin \alpha = 20.\sin {45^0} = 10\sqrt 2 \left( {m/s} \right)\\{a_y} = - g = - 10\,m/{s^2}\end{array}\end{array}\\{v_y} = 10\sqrt 2 - 10t\end{array} \right.\]

\( \Rightarrow y = 45 + 10\sqrt 2 t - 5{t^2}\,\,(m)\)

Phương trình quỹ đạo của vật là: \(y = 45 + x - \frac{{{x^2}}}{{40}}\)

\( \Rightarrow \) Vật có quỹ đạo là một Parabol

Khi lên đến độ cao max thì: 

v­_y = 0 \( \Rightarrow 10\sqrt 2 - 10t = 0 \Rightarrow t = \sqrt 2 \,(s)\)

Độ cao vật đạt được là: \(H = 45 + 10\sqrt 2 .\sqrt 2 - 5.{\left( {\sqrt 2 } \right)^2} = 55\,\,(m)\)

Khi vật chạm đất thì y = 0

\( \Rightarrow 45 + 10\sqrt 2 t - 5{t^2} = 0\,\, \Rightarrow t = 4,73\,s\)

Vậy sau 4,73s thì vật chạm đất

b. Tầm xa của vật: L = x = \(10\sqrt 2 .4,73 = 66,89\,(m)\)

Vận tốc vật khi chạm đất:

\(v = \sqrt {v_x^2 + v_y^2} = \sqrt {{{\left( {10\sqrt 2 } \right)}^2} + {{\left( {10\sqrt 2 - 10.4,73} \right)}^2}} = 36,05\,(m/s)\)

 c. Khi vật có độ cao 50 m thì

\(45 + 10\sqrt 2 t - 5{t^2} = 50\)

\( \Rightarrow \left[ {\begin{array}{*{20}{c}}{{t_1} = 0,414\,(s) \Rightarrow {v_{y1}} = 10\sqrt 2 - 10.0,414 \approx 10m/s}\\{{t_2} = 2,414\,(s) \Rightarrow {v_{y2}} = 10\sqrt 2 - 10.2,414 \approx - 10m/s}\end{array}} \right.\)

Tại t₁ vật đang đi lên, t₂ vật đang đi xuống.