Một người thợ mộc làm những cái bàn và những cái ghế. Mỗi cái bàn khi bán lãi 150 nghìn đồng, mỗi cái ghế khi bán lãi 50 nghìn đồng. Người thợ mộc có thể làm 40 giờ/tuần và tốn 6h làm 1 cái bàn, 3h làm 1 cái ghế. Khách hàng yêu cầu người thợ mộc làm số ghế ít nhất là gấp 3 lần số bàn. Một cái bàn chiếm chỗ bằng 3 cái ghế và ta có phòng để được nhiều nhất 4 cái bàn/tuần. Hỏi người thợ mộc phải sản xuất như nào để có tiền lãi thu về là lớn nhất.

Gọi x, y lần lượt là số bàn và số ghế mà người thợ mộng sản xuất trong một tuần, (x, y ≥ 0)

Số tiền lãi mà người thợ thu được trong một tuần là: 

150x + 50y (nghìn đồng)

Theo bài ta có:

\(\left\{ \begin{array}{l}6x + 3y \le 40\\y \ge 3x\\x + \frac{y}{4} \le 4\\x \ge 0\\y \ge 0\end{array} \right.\)⇔ \(\left\{ \begin{array}{l}6x + 3y \le 40\\y \ge 3x\\4x + y \le 16\\x \ge 0\\y \ge 0\end{array} \right.\left( I \right)\)

Vẽ miền nghiệm của (I) ta có miền nghiệm đó là miền tứ giác ABCO trong đó:

\(A\left( {0;\frac{{40}}{3}} \right),B\left( {\frac{4}{3};\frac{{32}}{3}} \right),C\left( {\frac{{16}}{7};\frac{{48}}{7}} \right),O\left( {0;0} \right)\)

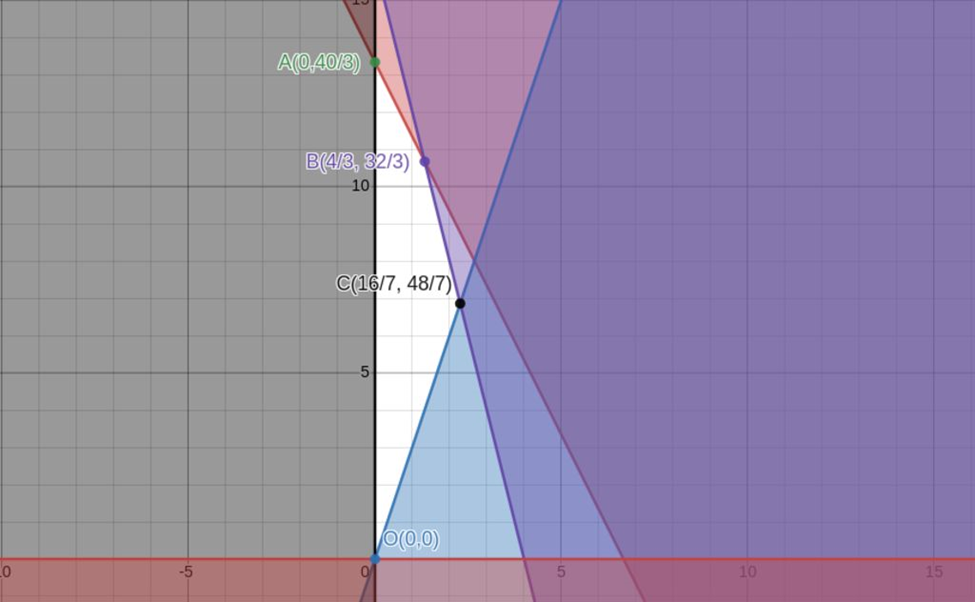
Đặt F(x; y) = 150x + 50y

Suy ra: \(F\left( A \right) = \frac{{2000}}{3};F\left( B \right) = \frac{{2200}}{3};F\left( C \right) = \frac{{4800}}{7};F\left( O \right) = 0\)

Vậy F(x; y)_max = F(B) = \(\frac{{2200}}{3}\)khi \(x = \frac{4}{3};y = \frac{{32}}{3}\).