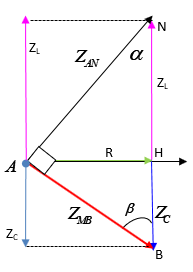
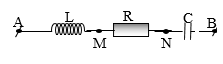
Một đoạn mạch điện AB gồm cuộn dây thuần cảm có độ tự cảm L, điện trở thuần R và
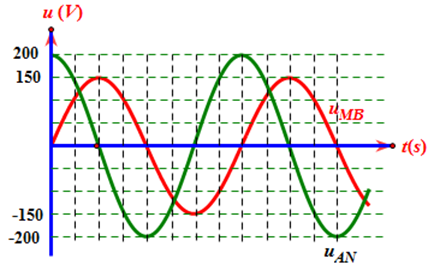
Một đoạn mạch điện AB gồm cuộn dây thuần cảm có độ tự cảm L, điện trở thuần R và tụ điện C mắc nối tiếp theo đúng thứ tự trên, M là điểm nối giữa cuộn cảm L và điện trở R, N là điểm nối giữa R và tụ điện \[C\]. Cho đồ thị biểu diễn sự phụ thuộc theo thời gian của các điện áp tức thời uAN, uMB như hình vẽ. Biết \[R = 120\;\Omega \]. Công suất tiêu thụ của đoạn mạch và dung kháng của tụ có giá trị nào sau đây?
B. \(60\;{\rm{W}};90\;\Omega \).