Một chất điểm dao động điều hòa trên trục Ox với chu kỳ 1,2 s. Tại thời điểm
36
24/05/2024
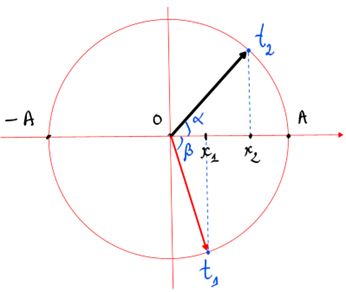
Một chất điểm dao động điều hòa trên trục \(Ox\) với chu kỳ 1,2 s. Tại thời điểm \({t_1}\) chất điểm có ly độ \({x_1} = 2\sqrt 5 \;cm\) và tại thời điểm \({t_2} = {t_1} + 1,5(s)\) chất điểm có ly độ \({x_2} = 4\sqrt 5 \;cm\). Chiều dài quỹ đạo là
A. \(10\;cm\)
B. \(20\;cm\)
C. 30 cm
Trả lời
Ta có:
Suy ra, vecto biểu diễn dao động \({x_1}\)vuông góc với vecto biểu diễn dao động \({x_2}\)nên ta luôn có biểu thức sau đây:
\({(\frac{{{x_1}}}{A})^2} + {(\frac{{{x_2}}}{A})^2} = 1 \Rightarrow x_1^2 + x_2^2 = {A^2} \Rightarrow A = 10(cm)\)
Suy ra, chiều dài quỹ đạo là: L=2.A=20(cm)
Chọn đáp án B
Lưu ý: Chứng minh biểu thức độc lập thời gian của 2 vecto vuông góc với nhau
