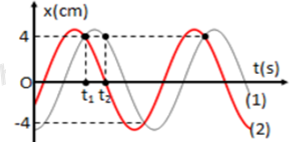
Một chất điểm có khối lượng 200 g thực hiện đồng thời hai dao động điều hòa cùng tần số, cùng biên độ có li độ phụ thuộc thời gian được biễu diễn như hình vẽ. Biết t2 − t1 = 13 s. Lấy π2 = 10

Lời giải
Từ đồ thị ta có:
+ Tại thời điểm t1: x2 = 4 cm↓ và x1 = 4 cm↑
+ Tại thời điểm t2: x2 = 0 cm↓ và x1 = 4 cm↓
Gọi A và φ là biên độ dao động và độ lệch pha của hai dao động thành phần.
Biểu diễn trên VTLG ta có:
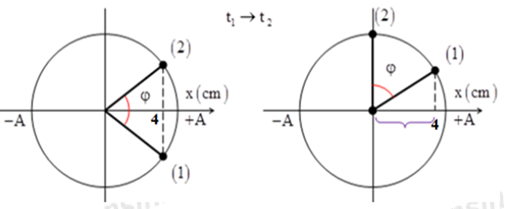
Từ VTLG, ta có: \(\left\{ \begin{array}{l}\cos \frac{\varphi }{2} = \frac{4}{A}\\\sin \varphi = \frac{4}{A}\end{array} \right. \Rightarrow \cos \frac{\varphi }{2} = \sin \varphi \)
\( \Leftrightarrow \cos \frac{\varphi }{2} = \cos \left( {\varphi - \frac{\pi }{2}} \right) \Rightarrow \varphi = \frac{\pi }{3} \Rightarrow A = \frac{8}{{\sqrt 3 }}\left( {cm} \right)\)
Biên độ dao động tổng hợp hai dao động thành phần là:
\({A_{th}} = \sqrt {{A^2} + {A^2} + 2.A.A.\cos \varphi } = 8\left( {cm} \right) = 0,08\left( m \right)\)
Ta có: \(\varphi = \frac{\pi }{3} \Rightarrow {t_{1 \to 2}} = \frac{\varphi }{\omega } = \frac{{\frac{\pi }{3}}}{{\frac{{2\pi }}{T}}} = \frac{T}{6}\)
\({t_2} - {t_1} = \frac{T}{6} = \frac{1}{3}\left( s \right) \Rightarrow T = 2\left( s \right)\)
Cơ năng của chất điểm có giá trị bằng: \[{\rm{W}} = \frac{1}{2}m{\omega ^2}{A^2} = {6,4.10^{ - 3}}\left( J \right) = 6,4\left( {mJ} \right)\]
Đáp án đúng: D