Hàm số y = f(x^2 + 2x) nghịch biến trên khoảng nào x - vô cùng -2 1 3 + vô cùng
Hàm số y = f(x2 + 2x) nghịch biến trên khoảng nào?
|
x |
–∞ |
–2 |
1 |
3 +∞ |
|
f'(x) |
– |
0 + |
0 – |
0 – |
y = f(x2 + 2x)
y' = (2x + 2)f'(x2 + 2x)
Xét y' = 0 ta có: (2x + 2)f'(x2 + 2x) = 0
⇒ \(\left[ \begin{array}{l}2x + 2 = 0\\f'\left( {{x^2} + 2x} \right) = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 1\\{x^2} + 2x = - 2\\{x^2} + 2x = 1\\{x^2} + 2x = 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 1\\x = - 3\\x = - 1 + \sqrt 2 \\x = - 1 - \sqrt 2 \end{array} \right.\)
Ta có bảng biến thiên:
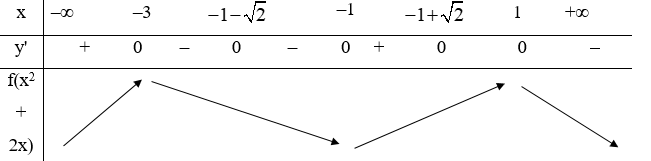
Vậy hàm số nghịch biến trên (–3; –1) và (1; +∞)