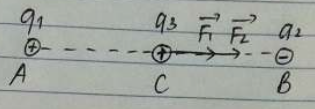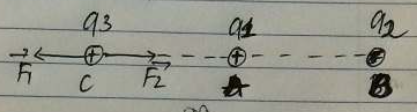Hai điện tích q1; = 8.10^ - 8C và q2 = - 8.10^ - 8C đặt tại A và B trong không khí cách nhau một khoảng AB = 6 cm. Xác định lực điện tác dụng lên q3 = 8.10^ - 8C đặt tại C nếu: a) CA = 4 cm
Hai điện tích q1=8.10−8C và q2=−8.10−8C đặt tại A và B trong không khí cách nhau một khoảng AB = 6 cm. Xác định lực điện tác dụng lên q3=8.10−8C đặt tại C nếu:
a) CA = 4 cm và CB = 2 cm;
b) CA = 4 cm và CB = 10 cm;
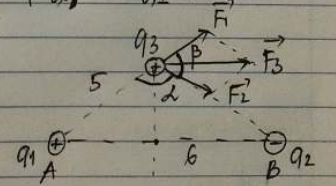
c) CA = CB = 5 cm.