Gọi x0,y0,z0 là ba số thực dương sao cho biểu thức P= 3/2x+y+ căn8yz -8/ căn 2(x^2+y^2+z^2)+4xz+3- 1/x+y+z đạt giá trị nhỏ nhất.
Gọi là ba số thực dương sao cho biểu thức
đạt giá trị nhỏ nhất.
Tổng bằng
A. 3
B. 1
C.
D.
Gọi là ba số thực dương sao cho biểu thức
đạt giá trị nhỏ nhất.
Tổng bằng
A. 3
B. 1
C.
D.
Hướng dẫn giải
Ta có
.
Đặt . Khi đó .
Ta có .
Bảng biến thiên
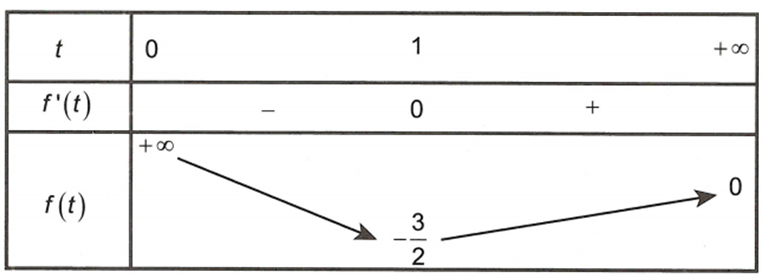
Suy ra . Dấu “=” xảy ra .
Do đó Chọn B.