Gọi M là điểm bất kì trên đoạn thẳng AB. Vẽ về một phía của AB các hình vuông
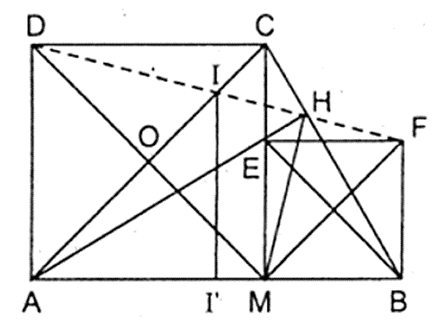
Gọi M là điểm bất kì trên đoạn thẳng AB. Vẽ về một phía của AB các hình vuông AMCD, BMEF.
a) Chứng minh rằng AE ⊥ BC.
b) Gọi H là giao điểm của AE và BC Chứng minh rằng ba điểm D,H, F thẳng hàng.
c) Chứng minh rằng đường thẳng DF luôn luôn đi qua một điểm cố định khi điểm M chuyển động trên đoạn thẳng AB cố định.