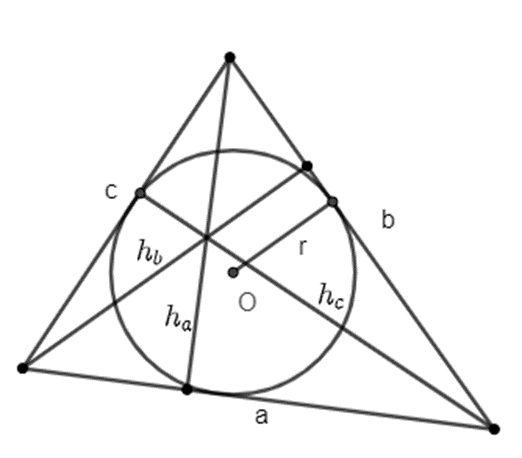
Gọi a, b, c lần lượt là ba cạnh của tam giác; ha, hb, hc lần lượt là các đường cao tương ứng với ba cạnh đó và r là bán kính đường tròn nội tiếp tam giác đó. Chứng minh rằng: \(\frac{1}{{{h_a}}} + \frac{1}{{{h_b}}} + \frac{1}{{{h_c}}} = \frac{1}{r}\).
Ta có:
\(S = \frac{1}{2}a.{h_a} \Rightarrow \frac{1}{{{h_a}}} = \frac{a}{{2S}}\);
\(S = \frac{1}{2}b.{h_b} \Rightarrow \frac{1}{{{h_b}}} = \frac{b}{{2S}}\);
\(S = \frac{1}{2}c.{h_c} \Rightarrow \frac{1}{{{h_c}}} = \frac{c}{{2S}}\).
Do đó: \(\frac{1}{{{h_a}}} + \frac{1}{{{h_b}}} + \frac{1}{{{h_c}}} = \frac{{a + b + c}}{{2S}} = \frac{{2p}}{{2S}} = \frac{p}{S} = \frac{p}{{p.r}} = \frac{1}{r}\).
Hay \(\frac{1}{{{h_a}}} + \frac{1}{{{h_b}}} + \frac{1}{{{h_c}}} = \frac{1}{r}\) (đpcm).