Giữa hai bến sông A, B có hai tàu chuyển thư chạy thẳng đều. Tàu đi từ A chạy xuôi dòng, tàu đi từ B chạy ngược dòng. Khi gặp nhau và chuyển thư, mỗi tàu tức thì trở lại bến xuất phát. Nếu kh

Trả lời

Lời giải

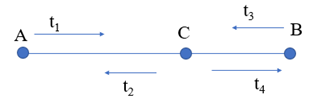
Gọi C là điểm gặp nhau, v là vận tốc dòng nước.

Theo đề bài: vận tốc 2 tàu so với dòng nước bằng nhau, ta gọi là V

Vì hai tàu xuất phát cùng lúc và gặp nhau tại C nên t₁ = t₃ (1)

Sau đó, 2 tàu quay trở lại tổng thời gian tàu A đi là 3 h, tàu B đi là 1,5 h.

t₁ + t₂ = 3 h

t₃ + t₄ = 1,5 h

Thời gian đi của tàu từ A tới C: \({t_1} = \frac{{AC}}{{V + v}}\)

Thời gian về của tàu từ C tới A: \({t_2} = \frac{{AC}}{{V - v}}\)

Thời gian tàu đi từ A cả đi lẫn về là

\({t_1} + {t_2} = 3 \Leftrightarrow \frac{{AC}}{{V + v}} + \frac{{AC}}{{V - v}} = AC\left( {\frac{1}{{V + v}} + \frac{1}{{V - v}}} \right)\, = 3\) (2)

Thời gian đi của tàu từ B tới C: \({t_3} = \frac{{BC}}{{V - v}}\)

Thời gian về của tàu từ C tới B: \({t_4} = \frac{{BC}}{{V + v}}\)

Thời gian tàu đi từ B cả đi lẫn về là

\({t_3} + {t_4} = 1,5 \Leftrightarrow \frac{{BC}}{{V - v}} + \frac{{BC}}{{V + v}} = BC\left( {\frac{1}{{V - v}} + \frac{1}{{V + v}}} \right) = 1,5\) (3)

Từ (2), (3) \( \Rightarrow AC = 2BC\) \( \Rightarrow AC = \frac{2}{3}AB\) thay vào (1) được:

Mà thời gian đi của tàu từ A tới C bằng thời gian đi của tàu từ B tới C nên

\(\frac{{AC}}{{V + v}}\)\( = \frac{{BC}}{{V - v}}\) \( \Rightarrow V = 3v\)

Thay \(AC = \frac{2}{3}AB\) và V = 3v vào (2)

\(\frac{2}{3}AB\left( {\frac{1}{{4v}} + \frac{1}{{2v}}} \right)\, = 3 \Rightarrow AB = 6v\)(4)

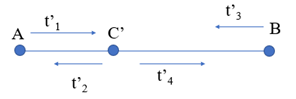
Để thời gian cả đi lẫn về của hai tàu như nhau thì hai tàu gặp nhau ở vị trí C’

t’₁ + t’₂ = t’₃ + t’₄

\( \Rightarrow \frac{{AC'}}{{V + v}} + \frac{{AC'}}{{V - v}} = \frac{{BC'}}{{V - v}} + \frac{{BC'}}{{V + v}} \Rightarrow AC' = BC' = \frac{{AB}}{2}\)

Khi xuất phát tàu B xuất phát trước tàu A một khoảng t₀, ta có:

\(t_3^' - t_1^' = {t_0}\)\( \Rightarrow \frac{{BC'}}{{V - v}} - \frac{{AC'}}{{V + v}} = {t_0}\)

\( \Rightarrow BC'\left( {\frac{1}{{V - v}} - \frac{1}{{V + v}}} \right) = {t_0} \Rightarrow \frac{{AB}}{2}\left( {\frac{1}{{2v}} - \frac{1}{{4v}}} \right) = {t_0}\)

Thay (4) vào \( \Rightarrow {t_0} = \frac{{6v}}{2}.\frac{1}{{4v}} = 0,75\,h\)

Vậy tàu A phải xuất phát muộn hơn tàu B là 0,75 h = 45 phút