Giải phương trình x^2 - 1 = 2 căn bậc hai của 2x + 1
Giải phương trình x2−1=2√2x+1.
Lời giải
Ta có:
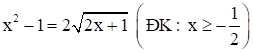
⇔x2−1+2x+2=2√2x−1+2x+2
⇔x2+2x+1=2x+1+2√2x+1+1
⇔(x+1)2=(√2x+1+1)2
⇔[x+1=√2x+1+1x+1=−(√2x+1+1)
⇔[x=√2x+1(1)x+√2x+1+2=0(2)
Giải (1): x=√2x+1⇔{x≥0x2=2x+1⇔{x≥0x2−2x−1=0
⇔{x≥0x2−2x+1−2=0⇔{x≥0(x−1)2=2
⇔{x≥0(x−1)2=2⇔{x≥0[x−1=√2x−1=−√2
⇔{x≥0[x=1+√2x=1−√2⇔x=1+√2
Kết hợp điều kiện x≥−12 ta có: x=1+√2.
Do đó phương trình (1) có 1 nghiệm là x=1+√2.
Giải (2): x+√2x+1+2=0
Với x≥−12 thì {√2x−1≥0x+2≥32⇒x+√2x+1+2>0
Do đó phương trình (2) vô nghiệm.
Vậy phương trình đã cho có tập nghiệm là S={1+√2}.