Giá trị nhỏ nhất của biểu thức $P=\left|1+2\cos x\right|+\left|1+2\sin x\right|$  bằng

Hướng dẫn giải

Ta có $P^2=6+4\left(\sin x+\cos x\right)+2\left|1+2\left(\sin x+\cos x\right)+4\sin x\cos x\right|$

Đặt $t=\sin x+\cos x=\sqrt{2}.\sin \left(x+\frac{\pi }{4}\right)$  với $\left|t\right|\le \sqrt{2}\Rightarrow \sin x\cos x=\frac{t^2-1}{2}$

Xét $y=P^2=6+4t+2\left|2t^2+2t-1\right|=\left\{\begin{array}{l}4t^2+8t+4khit\le \frac{-1-\sqrt{3}}{2};t\ge \frac{-1+\sqrt{3}}{2}\\ -4t^2+8khi\frac{-1-\sqrt{3}}{2}<t<\frac{-1+\sqrt{3}}{2}\end{array}\right.$

$\Rightarrow y^{\text{'}}=\left\{\begin{array}{l}8t+8khit<\frac{-1-\sqrt{3}}{2};t>\frac{-1+\sqrt{3}}{2}\\ -8tkhi\frac{-1-\sqrt{3}}{2}<t<\frac{-1+\sqrt{3}}{2}\end{array}\right.$

Bảng biến thiên

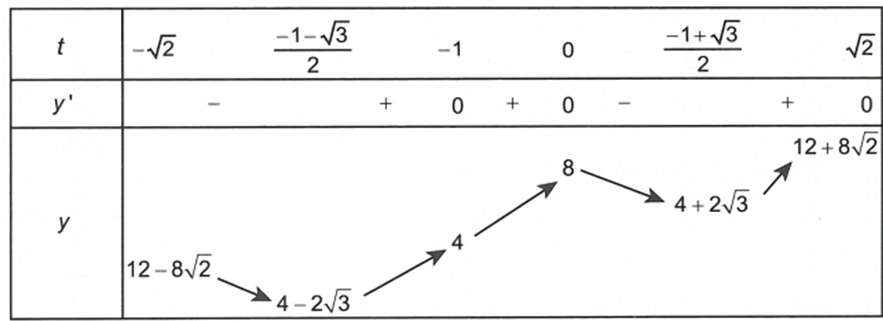
Dựa vào bảng biến thiên, suy ra $\underset{\left[-\sqrt{2};\sqrt{2}\right]}{\min }f\left(t\right)=4-2\sqrt{3}={\left(\sqrt{3}-1\right)}^2$

$\Rightarrow \min P=\sqrt{3}-1$

Chọn B