Giá trị nào của m để điểm I(−1; 6) là điểm cực đại của đồ thị hàm số y = x^3 − 3mx^2 − 9x + 1 (Cm).

Trả lời

Lời giải

Ta có $y' = 3{x^2} - 6mx - 9$.

Để I(−1; 6) là điểm cực đại của đồ thị hàm số y = x³ − 3mx² − 9x + 1 (Cm) thì trước hết x = −1 là nghiệm của phương trình 3x² − 6mx − 9 = 0.

Û 3(−1)² − 6m(−1) − 9 = 0

Û 3 + 6m − 9 = 0

Û m = 1.

Thử lại với m = 1 ta được:

$y = {x^3} - 3{x^2} - 9x + 1$ (Cm)

Khi đó với x = −1 ta có y = 6. Vây I(−1; 6) là điểm thuộc đồ thị hàm số.

Lại có $y' = 3{x^2} - 6x - 9 = 3\left( {x + 1} \right)\left( {x - 3} \right) = 0$

$\Rightarrow \left[ \begin{array}{l}x + 1 = 0\\x - 3 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 3\end{array} \right.$

Ta xét BBT:

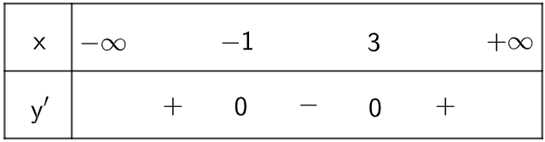
Dựa vào BBT ta thấy x = −1 là điểm cực địa của đồ thị hàm số

Vậy để điểm I(−1; 6) là điểm cực đại của đồ thị hàm số y = x³ − 3mx² − 9x + 1 (Cm) thì m = 1.